
arXiv Preprint
Robert L. Foote
Selected Papers
Geometry of the tracks left by a bicycle is closely related to the so-called Prytz planimeter and with linear fractional transformations of the complex plane. We describe these relations, along with the history of the problem, and give a proof of a conjecture made by Menzin in 1906. Reprint
Infinitesimal
Isometries
Along Curves and Generalized Jacobi Equations
with C.K. Han and J.W. Oh
J Geometric Analysis, 23
(2013) 377–394
The Volume Swept Out by a Moving Planar Region
Mathematics Magazine, 79 (2006) 289-297.
A result is presented, evidently due to Courant, about the connection between the volume swept out by a moving planar region and the motion of its centroid. This generalizes both the Theorem of Pappus and Cavalieri's Principle. Reprint
The Dynamics of Pendulums on Surfaces of
Constant Curvature
with P. Coulton and G. Galperin

Integral-Geometric Formulas for Perimeter in S2,
H2, and Hilbert Planes
with Ralph Alexander and I.D. Berg
Rocky Mountain Journal of Mathematics, 35 (2005) 1825-1860
Geometry of the Prytz Planimeter
Reports on Mathematical Physics, 42 (1998) 249-271
Planimeters and Isoperimetric Inequalities on Constant
Curvature Surfaces
In preparation. Preliminary
version
available.
Abstract. A planimeter is a mechanical instrument used to determine the area of a region in the plane. As the boundary of the region is traced, a wheel attached to the instrument partially rolls and partially slides, recording a component of its motion on the plane. The area of the region is a simple function of the net roll of the wheel. We show how the analogue of this instrument works on the sphere and the hyperbolic plane, and then use the results to give a simple proof of one of the Bonnesen isoperimetric inequalities for these surfaces. The rolling of the wheel can be interpreted as parallel translation for a connection in a certain bundle over the surface. The isoperimetric inequality can then be viewed as a statement about the holonomy of this connection.
Presented at Lehigh Geometry/Topology Conference, June 1997
Dynamic, Interactive Hyperbolic Geometry with PoincaréDraw
An account of the motivation for and development of the computer program PoincaréDraw. Unpublished. Written for the conference "Exploring Undergraduate Algebra & Geometry with Technology" held at DePauw University, June 1996.
Close Encounters with Mathematical Cranks of the Third Kind
review of
Mathematical Cranks and A Budget of Trisections (renamed
The Trisectors) by Underwood Dudley
Skeptical Inquirer,
Vol.18, Winter 1994, 182-186.
For better or for worse, pseudo-mathematics does not share the popularity among cranks that other subjects seem to have. It just doesn't have the same appeal as parapsychology, astrology, or UFOs. Nevertheless, mathematical cranks do exist, as mathematics departments at many major universities are well aware. When I was a graduate student at the University of Michigan, it was not uncommon for the departmental mailboxes to be stuffed periodically with the local crank's most recent proof of the rationality of p or the square root of 2.
While most crank mathematics winds up in the wastebasket (frequently after serving as departmental entertainment), occasionally a well-meaning mathematician makes the mistake of responding to a crank, pointing out his errors, hoping to set him straight. Thus may begin a series of communications between crank and mathematician (mostly from crank to mathematician), usually ending when the mathematician is forced to be rude, or the crank becomes angry and goes in search of a more "tolerant" mathematician. The moral of the story is, don't get involved with a crank.
While frequently giving this advice to others, Underwood Dudley, professor of mathematics at DePauw University in Greencastle, Indiana, has made it his professional hobby to collect the works of modern mathematical cranks, to correspond with them, and even to meet them. In these two books, he shares his fascinations and frustrations with people bent on pseudo-mathematics.
What types of things do mathematical cranks work on? Most of Dudley's examples can be placed into two broad categories: 1) real mathematics that has been twisted, misunderstood, or has had its significance horribly exaggerated, and 2) impenetrable nonsense.Excerpt from the review.
Vector Bundles Over Homogeneous Spaces and Complete Locally
Symmetric Spaces
with Lance
D.
Drager
Proceedings of Symposia in Pure Mathematics, 54
(1993), Part 2, Green and Yau, eds., 183--189.

A Geometric Solution to the Cauchy Problem for the
Homogeneous Monge-Amperè Equation
Proc. Workshops
in Pure Math. Vol. 11,
1991, 31--39, Korean Acad. Council.
Observing the Heat Equation on a Torus Along a
Dense Geodesic
with L. D. Drager and C. F. Martin
Sys. Sci. and Math. Sci., 4 (1991) 186--192
Abstract.
Several
authors have considered observability problems for the heat
equation and related partial differential equations. A basic
problem is to determine what kinds of sampling provide sufficient
information to uniquely determine the initial heat distribution.
We address the case where the temperature is measured while
traveling along a curve.
We consider the special
case where the space is a flat torus (of arbitrary dimension) and
the curve is a geodesic. It is shown that, in this case, the
observed temperature is sufficient information to uniquely
determine the initial heat distribution if and only if the
geodesic is dense in the torus.
In the case of a torus,
Fourier analysis techniques can be used to write down the solution
of the heat equation. This allows us to derive an explicit
representation of the observed temperature in terms of the initial
distribution. We use this representation and some ideas from the
theory of almost periodic functions to show that the Fourier
coefficients of the initial distribution can be recovered from the
observation.
Homogeneous Complex Monge-Amperè Equations and
Algebraic Embeddings of Parabolic Manifolds
Indiana Univ Math. J., 39 (1990) 1245-1273
Controllability of Linear Systems, Differential Geometry of
Curves in
Grassmannians and Generalized Grassmannians, and Riccati
Equations
with Lance D. Drager, Clyde F. Martin, and James Wolper
Acta Appl. Math., 16 (1989) 281-317

Observing Ergodic Translations on Compact Abelian Groups
with Discontinuous Functions
with L.D. Drager and D. McMahon
IMA J. Math.
Control & Info., 6 (1989)
441--463
Abstract.
Several authors have considered the problem of global
observability for minimal dynamical systems, and particularly the
example of ergodic (equivalently, minimal) translations on compact
abelian groups. The global observability problem for ergodic
translations is considered here in the case where the output
function may be discontinuous. The result for continuous output
functions, essentially due to McMahon, is described. This result
shows that a continuous output function observes all ergodic
translations if and only if it has no nontrivial symmetries. This
result is extended here in two directions.
First, functions
continuous except on a meagre set and symmetries modulo
meagre sets are considered. A result analogous to the continuous
case is obtained that includes and generalizes the continuous case
and results of Balogh, Bennett, and Martin on observing ergodic
translations with the characteristic functions of certain subsets
of the group. Functions continuous except on a set of measure zero
are also considered.
Secondly, ergodic
theory and harmonic analysis techniques are employed to consider
the case of integrable output functions and symmetries modulo sets
of measure zero. It is shown that an integrable function observes
ergodic translations modulo sets of measure zero if and only if it
has no nontrivial symmetries modulo sets of measure zero.
The group of symmetries
of the output function modulo sets of measure zero can be
determined from its Fourier series. The results here show that
classical observability can be determined from the Fourier series
when the function is continuous almost everywhere, but only
observability modulo sets of measure zero can be determined when
the output function is merely integrable.
Differential Geometry of Real Monge-Amperè Foliations
Mathematische Zeitschrift, 194 (1987) 331-350
Abstract. The foliations studied in this paper are those that arise from the Monge-Amperè condition requiring the Hessian of a function defined on an affine manifold to have rank that is one less than maximal. The real, homogeneous Monge-Amperè equation is det H(u) = 0, where u is a real-valued function on an open subset of Rn. Solutions that satisfy rank H(u) = n-1 induce a foliation of the domain of u by lines. The standard solution is u(x) = ||x||, which satisfies rank H(u) = n-1. The standard solution is characterized in three ways using the geometric "twist" of the foliation, the covariant derivatives of H(u), and strictly convex exhaustions of the domain of u. The Cauchy problem for det H(u) = 0 is treated.
The Contraction Mapping Lemma and the Inverse Function
Theorem in Advanced Calculus
with Lance D. Drager
Amer. Math. Monthly, 93 (1986) 52-54
Abstract. The most elegant and general proof of the inverse function theorem uses the contraction mapping lemma. In an advanced calculus course, time does not generally permit a proof of the contraction mapping lemma as it is usually formulated. We give a simple proof of the contraction mapping lemma in Rn based on the max/min principle, familiar to calculus students -- a continuous, real-valued function defined on a non-empty, closed, bounded subset of Rn attains its maximum and minimum on that set -- thus allowing the general proof of the inverse function theorem usually left for more advanced courses.
Regularity of the Distance Function
Proc. Amer. Math. Soc., 92 (1984) 153-155
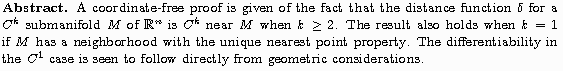
Curvature Estimates for Monge-Amperè Foliations
Ph.D. Dissertation, University of Michigan, 1983
Abstract.
The foliations studied in this paper are those that arise from the
Monge-Amperè condition that requires the Hessian of a
real-valued function to have rank that is one less than maximal.
In the first chapter,
the geometry of the foliations of Rn is studied. The
main theorems are the two characterizations of the standard
foliation.
In the second chapter,
the foliations of complex manifolds are studied. The locally
Reinhardt foliations are those to which the geometry and
methods of the first chapter can be applied directly. Hörmander's L2-∂ technique
is used to relate the geometry and the analysis of a Stein
manifold that admits such a foliation outside a compact set. The
main result is the embedding theorem of the last section.