This is a small-amplitude oscillation about the stable equilibrium. The period is essentially 2 pi R.


Pendulum Motion Due to Curvature
The Pendulum on S2
All of these have d/R = 2/5.
theta(0) = .1, theta'(0) = 0
This is a small-amplitude oscillation about the stable equilibrium. The period
is essentially 2 pi R.


theta(0) = 1.5, theta'(0) = 0
This is a large oscillation about the stable equilibrium.


The next three start at the stable equilibrium with different values of
theta'(0) illustrating that theta'(0) = 1 separates oscillatory and orbital
behavior.
theta(0) = 0, theta'(0) = .99


theta(0) = 0, theta'(0) = 1


theta(0) = 0, theta'(0) = 1.01


The Pendulum on H2
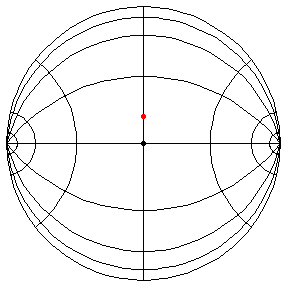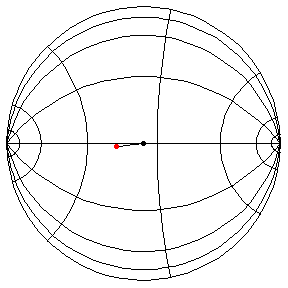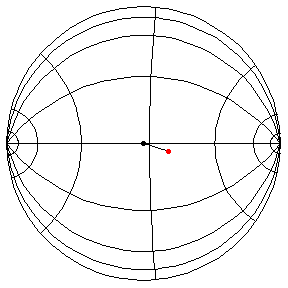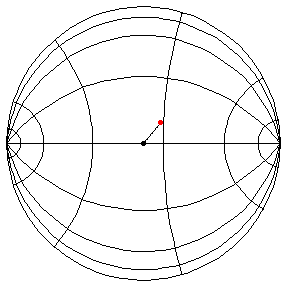
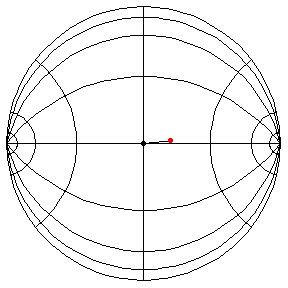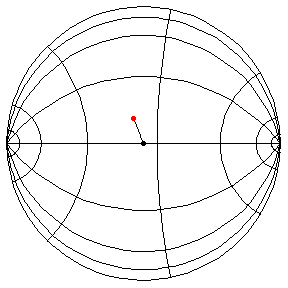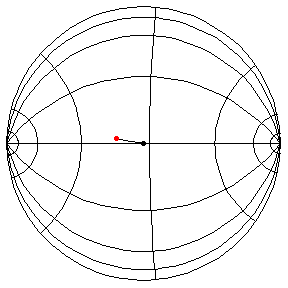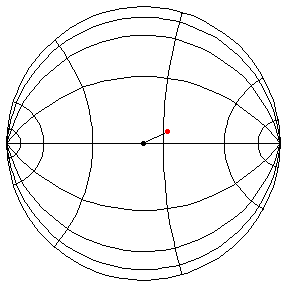
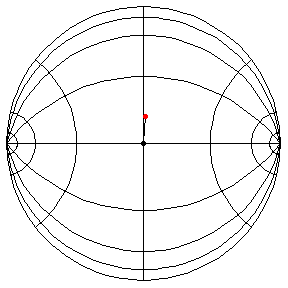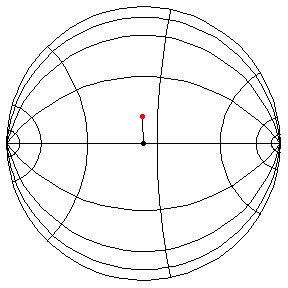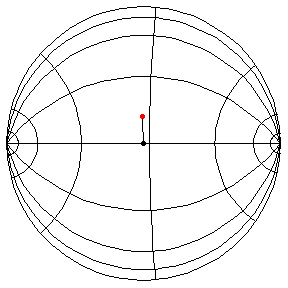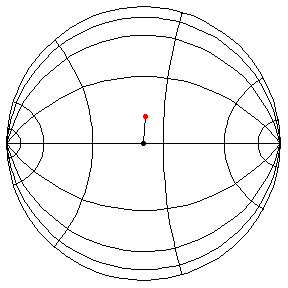
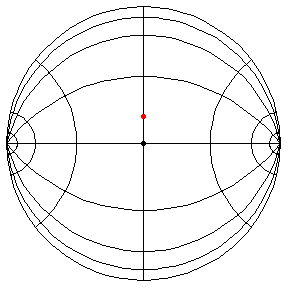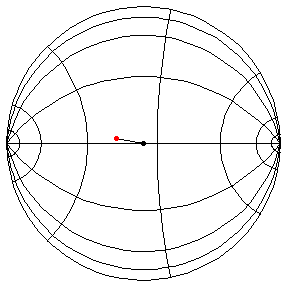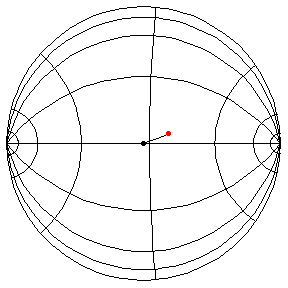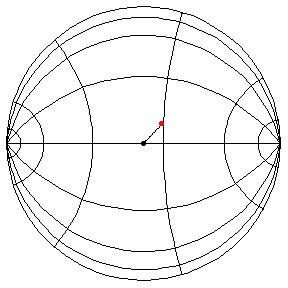
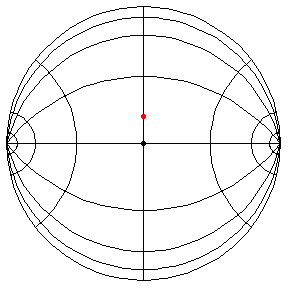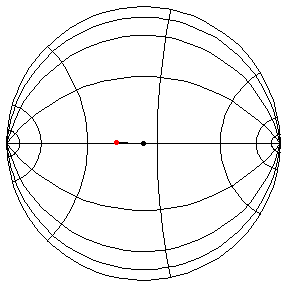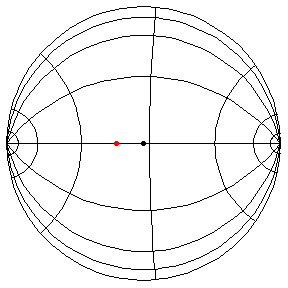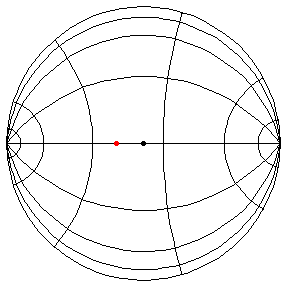
These are in the Poincare disk model. The horizontal line through the center is the geodesic along which the pivot travels. The other horizontal curves are equally-spaced equidistant curves. The vertical curves are equally spaced geodesics perpendicular to the path of the pivot. (This situation is identical to that on S2.) All of these have d/R = 2/5.
theta(0) = .1, theta'(0) = 0
This is a large oscillation about the stable equilibrium.
theta(0) = 1.5, theta'(0) = 0
This is a small-amplitude oscillation about the stable equilibrium. The period
is essentially 2 pi R.
The next three start at the stable equilibrium with different values of
theta'(0) illustrating that theta'(0) = 1 separates oscillatory and orbital
behavior.
theta(0) = pi/2, theta'(0) = .99
theta(0) = pi/2, theta'(0) = 1
theta(0) = pi/2, theta'(0) = 1.01