Using a Prytz Planimeter to Measure Area
Area is measured, but only approximately. When the tracer
point T moves around a closed curve, the chisel edge C follows
a zig-zag path. When the tracer point returns to the base point B,
the chisel edge C has undergone a net rotational displacement s.
Multiply s by the length l of the planimeter
and you get the area of the region!
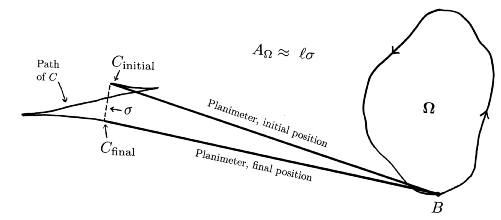If this sounds too good to be true, you're right, but the error has a very
nice geometric interpretation. As the tracer point goes counterclockwise
around the boundary of the region W being measured
starting and stopping at B, the chisel edge C traces parts
of two nearly triangular regions. The the circular arc of length
s
forms the remaining sides of these triangles. Note that C
traces the upper triangle in the clockwise (CW) direction and the lower one in
the counterclockwise (CCW) direction. It turns out that the product
ls equals the area A of W
plus the area of the CW triangle
minus the area of the CCW
triangle. In symbols (and solved for AW),
AW = ls
+ ACCW - ACW .
Why this is true.
It follows that the error made by using ls
as an approximation for the area of W is the
difference between the areas of these triangular regions. By carefully
choosing the starting position of the planimeter, you can measure areas
fairly accurately with this simple device! It also turns out that
the error is inversely proportional to the length of the planimeter, so
measuring a small region with a large planimeter is more accurate.
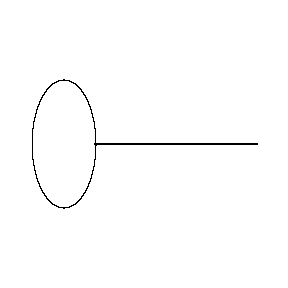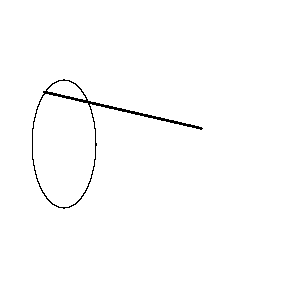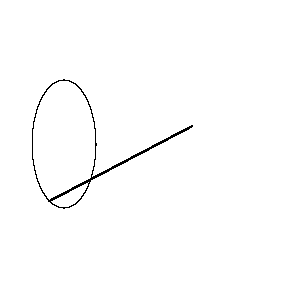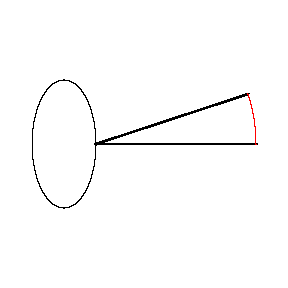
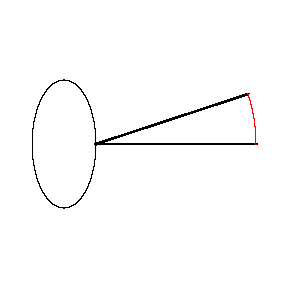
Here is an ellipse with major diameter 4 and minor diameter 2 being
measured by a planimeter of length 5. The picture on the right shows
the initial and final positions of the planimeter, and the circular arc
between them (in red).
The length of the circular arc is about 1.59. Multiplying by the
length of the planimeter yields 7.94 as an approximation of the area of
the ellipse. The real area is, of course, 2pi, or about 6.28, so
the approximation is a whopping 26% too big! Measuring the ellipse
with a longer planimeter gives a better approximation. For example,
a planimeter of length 10 gives an approximation of 7.00 for the area,
which is 11% too big. One of length 20 gives an approximation of
6.62 for the area, only 5.3% too big.
Changing the initial direction of the planimeter makes a difference
in the result. If the planimeter of length 5 starts pointing down
instead of to the right (still starting at the same point on the ellipse),
the approximation for the area is 6.77, which is only 7.8% too large.
If it starts pointing to the left, the approximation for the area is 5.23,
which is 17% too small.
Goodman's variation. When using the planimeter, you usually
just measure the straight-line distance between the initial and final positions
of the chisel edge C, instead of the actual arc-length. In
1896 an engineer named Goodman designed a variation of Prytz's planimeter
by incorporating a curved scale into the bar. The radius of the curve
equals the length of the planimeter, and so the arc-length between the
inital and final positions of the chisel can be measured directly from
this scale. This, however, does not correct the inherent inaccuracy
of the instrument.
Variation by Goodman 
Photo of an actual Goodman planimeter
