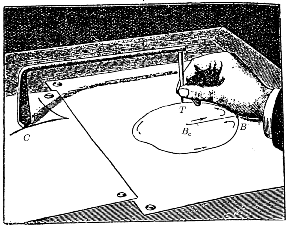
| It is a very simple device, consisting of a rod with its ends bent at right angles. One end, the tracer point T, is sharpened to a point, while the other end, C, is sharpened to a chisel edge parallel to the rod. The chisel edge is usually slightly rounded, making it look similar to a hatchet, and consequently the device is also known as a "hatchet planimeter." Prytz referred to it as a "stang planimeter," "stang" being Danish for "rod." |  |
 |
 |
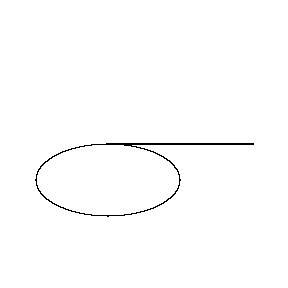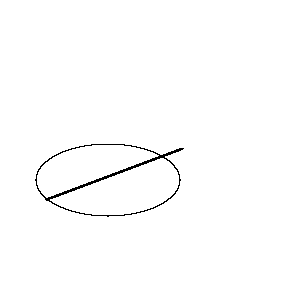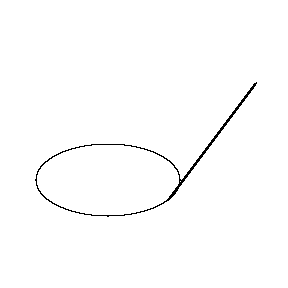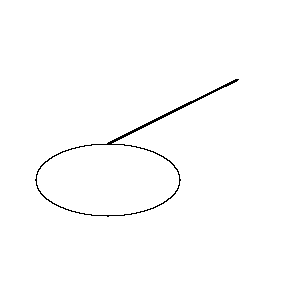 |
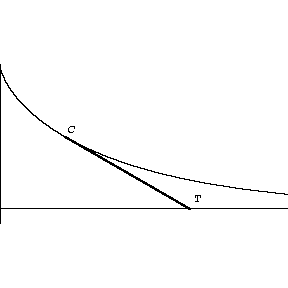
The tracer point goes around the ellipse. Note that the chisel point does not return to the point where it started. The angle between the initial and final positions of the chisel is roughly proportional to the area of ellipse. The constant of proportionality is the square of the length of the planimeter. The longer the planimeter, the more accurately the area is measured. |
| Main Planimeter Page |
Last update 1 August 2001
Robert
Foote |