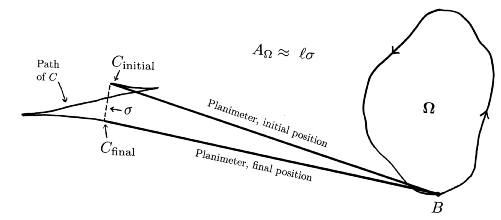
The claim is that the area A_W of the region W is given by

A_W  =  l s + A_CCW  - A_CW .

In this formula, l is the length of the planimeter, s is the length of the circular arc joining the initial and final positions of the chisel edge C, A_CW  is the area of the lower triangle traced clockwise by the chisel edge, and A_CCW  is the area of the upper triangle traced counterclockwise by the chisel edge.

To understand this, you first need to understand the how a general planimeter works.  If a planimeter rod with a wheel moves in such a way that both endpoints traverse closed curves, then the signed area swept out is given by the formula

A_R - A_L  =   l s  -  ¹/₂ l l ² Dq .

Here A_R and A_L are the signed areas traversed by the right and left endpoints, respectively, l is the length of the planimeter rod, s is the amount the wheel rolls, l is the parameter indicating the location of the wheel along the rod, and Dq  is the net rotation of the rod, which is a multiple of 2p.
    How do we apply this to a Prytz planimeter? Part of this is obvious -- take the right endpoint to be the tracer point, which goes around W, and so  A_R = A_W.  But the left endpoint doesn't go around a closed curve, and there's no wheel! Consider an imaginary wheel attached to the rod at the chisel edge. As the tracer point traces the boundary of W, the wheel doesn't turn, because its axis is parallel to the rod. Once the tracer point has returned to the base point B, imagine rotating the planimeter, moving the chisel edge from its final position back to its initial position. This would cause the wheel to roll by s. The left endpoint has now traversed a closed curve, and the signed area it encloses is and so A_L = A_CCW  - A_CW , and the net rotation is Dq  = 0.  Plugging into the signed are  formula above yields

A_W + A_CW  - A_CCW  =  l s ,

which was what we wanted to prove.

This proof is due to O. Henrici.