Why this page is viewed best with Internet Explorer or Sea Monkey

The following elegant proof of how a planimeter works is due largely to O. Henrici and can be found in

O. Henrici, Report on Planimeters, British Assoc. for the Advancement of Science, Report of the 64th meeting, 1894, pp. 496-523.

This paper also contains an interesting history of planimeters up through 1894.

I like this proof because it is almost entirely geometric, the algebra is minimal, and it can be understood intuitively without calculus. In addition, it shows how both linear and polar planimeters work independently of the linkages in their construction. Consequently, the explanation is valid for variants of these planimeters, which are used in a proof of the isoperimetric inequality.

Line Segments Sweeping Out Area
The Area Difference Theorem
Turning the Moving Segment Into a Planimeter
How the Roll of the Wheel is Related to Area
Combining the Area Difference Theorem and the Roll of the Wheel
Measuring a Region

Line Segments Sweeping Out Area

Planimeters work based on the intuitive notion of a moving line segment sweeping out area.  Here is a line segment sweeping out a narrow quadrilateral.  The segment is oriented by a vector N, which is normal, or perpendicular, to the segment.

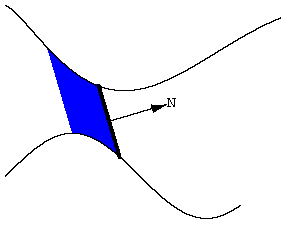The area swept out is signed, or oriented.  The positive direction is indicated by N.  Area swept out in the direction of N counts positively.

Area swept out in the direction opposite that of N counts negatively.

The Area Difference Theorem

Suppose the endpoints of an oriented moving line segment traverse closed curves in the counter clockwise direction.  The Moving Segment Theorem says that the signed area swept out by the segment is the difference between the areas enclosed by the curves, that is,  A = AR - AL ,   where AR and AL are the areas traversed by the right and left endpoints of the segment, respectively. The reason for this is very intuitive.

Turning the Moving Segment Into a Planimeter

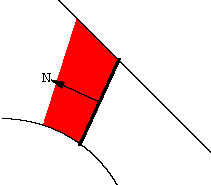The moving line segment becomes a planimeter by fixing its length and attaching a wheel (red).  The axis of the wheel is parallel to the segment.  The wheels are clearly seen on the schematics for the polar and linear planimeters, and on the underside of the carriage of my K&E polar planimeter. The surprising fact is that when a polar or linear planimeter is used to trace the boundary of a region, the amount the wheel rolls is proportional to the area of the region. Keep reading to see why.

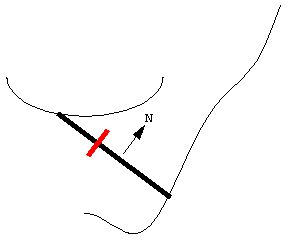Here is a planimeter moving with its ends following two curves. Even though the curves are different, the length of the planimeter doesn't change. As the planimeter moves, the wheel partially rolls and partially slides.  Motion of the segment in the direction of the vector N causes the wheel to roll, which is recorded on a scale attached to the wheel.  The motion of the segment along its length causes the wheel to slide, and this motion is not recorded. Thus the wheel records the component of motion in the direction perpendicular to the planimeter's length. The direction indicated by N is the direction in which area swept out counts positively -- it is not necessarily the direction of motion. In the animation, note that the left end of the planimeter has to move in reverse at one point in order to stay on its curve.

How the Roll of the Wheel is Related to Area

There are two basic types of movement of the planimeter.
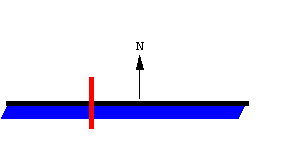
The first type of motion is when the planimeter moves parallel to itself, sweeping out a parallelogram. The important fact to note is that the roll of the wheel, which records the distance moved perpendicular to the rod, is exactly the height of the parallelogram. If A denotes the signed area swept out and s denotes the roll of the wheel, we get A = ls, where l is the length of the planimeter and the parallelogram. Note that if the planimeter moves in the direction opposite of N, the wheel rolls backwards. The equation above is still valid, but A and s are both negative.
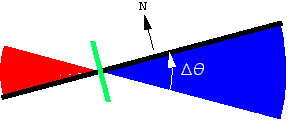	The second type of motion is when the planimeter rotates about the wheel. In this case part of the area swept out is positive and part of it is negative. Also note that the wheel doesn't roll! In this situation the net area swept out is related to the angle through which the planimeter rotates and the position of the wheel. The formula relating these is A = - 1/2 l l 2 Dq, which takes a little explanation.
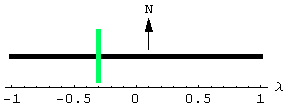
The wheel could be located at any point on the rod. The number l is between -1 and 1, and indicates the position of the wheel on the rod. At the right endpoint l = 1; at the left endpoint l = -1; at the midpoint l = 0. In the example shown here l = -3/10.
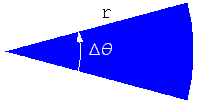	To get the formula for the signed area swept out, first recall that the area of a circular sector is A = 1/2 r2Dq.        If it is clear to you that A should depend linearly on l, note that A = - 1/2 l l2 Dq  must be the correct formula since it gives the right signed area for the values l = -1, 0, 1. If this isn't so clear, here is a more complete derivation.
The general motion of the planimeter is a combination of translations and rotations.  The signed area swept out is simply the sum of the translational and rotational parts.	A  =  l s  -  1/2 l l 2 Dq

Now suppose the planimeter rod moves so that it comes to rest in the same position in which it started. Then both formulas above for signed area (boxed in yellow) are valid, and so we get

When a planimeter is used to measure a region, the user moves the right endpoint of the rod, the tracing point, around the boundary of the region to be measured. Consequently the desired area is A_R. For a linear planimeter, the left endpoint moves back and forth along a line, enclosing no area, and so A_L = 0. Similarly, for a  polar planimeter used in the usual way, the left endpoint moves along the arc of a circle, but doesn't go completely around the circle; again A_L = 0. For both polar and linear planimeters used in the usual way, the planimeter rod doesn't make a full rotation, and so Dq = 0. Plugging these into the formula above boxed in green yields the simple formula for the area of the region being measured:

A_R  =   l s .

Three simple observations can be made from this.

• The area of the region is proportional to the amount the wheel rolls. The constant of proportionality is the length of the planimeter rod. The scale on the wheel takes this into account, allowing the user to simply read the quantity l s from the scale.

• It doesn't matter where the wheel is located along the rod.

• The left endpoint could follow any path that encloses no area -- polar and linear planimeters are just special cases.

A polar planimeter can be used to measure a large region by placing its pole inside the region. (The pole is the fixed endpoint of the pole arm -- also the center of the circle followed by the left endpoint of the tracer arm.) When used in this way, the left endpoint goes all the way around the circle it follows, and so A_L = pr², where r is the radius of this circle, that is, the length of the pole arm.  In addition, the tracer arm makes a full rotation, and so Dq = 2p. Inserting these into the above formula boxed in green yields

A_R  =   l s + pr² - lp l ²

for the area of the region being measured. The user reads the quantity l s from the scale and then adds pr² - lp l ² to get the desired area. The extra quantity added involves the lengths of the two planimeter arms and the location of the wheel. These are constants of the instrument, and are generally printed in the instruction manual.

Main Planimeter Page

Maintaining web pages with Greek letters is like trying to hit a moving target.  Internet Explorer and Mozilla Firefox used to support the same means for displaying Greek letters, but currently (May 2009) they do not. The Greek letters on this web page use a format that can be displayed by Internet Explorer and Sea Monkey.