 |
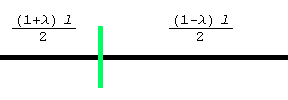 |
 |
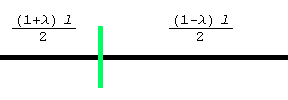 |
The area swept out consists of two circular sectors of different radii. The right and left radii are, respectively,(1-l) l /2 and (1+l) l /2. Noting that one of the signed areas is positive and the other is negative, we getA = 1/2 [(1-l) l /2] 2 Dq - 1/2 [(1+l) l /2] 2 Dq. Multiplying this out and simplifying yields A = -1/2 l l 2 Dq.