Planimeters and Isoperimetric Inequalities
Why this page is
viewed best
with Internet Explorer or Sea Monkey
 |
The isoperimetric inequality for a region in the plane
bounded by a
simple closed curve states that
L2 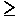 4pA,
4pA,
in which L is the length of the curve and A is
the area
of the region. It's easily seen that equality holds when the
curve
is a circle. In fact, equality holds only in this case.
There is a very simple and intuitive proof of the
isoperimetric inequality
based on how a planimeter works.
|
Proving the isoperimetric inequality requires tracing the boundary of
the
region with a planimeter in such a way that
- The tracer point goes around
the boundary of the region as usual,
- The curve followed by the opposite end
of the tracer arm encloses no area, and
- The planimeter
makes a full rotation in the process.
This puts a limitation on the
length of the planimeter that can be used.
Pictures
and animations showing how this can be done.
Now consider the
formula
AR
- AL
= l s -
1/2 l l 2 Dq
from how a planimeter works.
In this formula
- AR is the area enclosed by the tracer point;
in this case it is the area A of the region,
- AL is the area enclosed by the opposite end of
the tracer arm; as in the other applications, it
is 0,
- l is the length of the tracer arm,
- s is the roll of the wheel,
- l is a parameter determined by the location of the wheel;
in this case it is 1,
- Dq is the net rotation of the tracer arm; in this
case it is 2p.
Plugging these values in we get
A
=
l s - p l
2.
A little algebra (completing the square in l)
yields
s2 - 4pA = (A - pl 2)2/l 2 .
Now for a Key Observation: The roll of
the wheel, s, is less than
or equal to the length of the boundary, L. This is
because the wheel is at the tracer point, and it records only the
component of the motion of the tracer point that is perpendicular to
the tracer arm. It follows that
L2 - 4pA 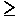 (A - pl
2)2/l 2. (A - pl
2)2/l 2. |
This is stronger than the desired result! We leave it
to the reader to ponder the geometric conditions under which equality
occurs.
To see that the region has to be a circle when L2
= 4pA,
consider the case when the length l of the tracer arm is the
radius r of the circumscribing
circle. We have
L2 - 4pA 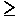 (A - pr2)2/r2.
(A - pr2)2/r2.
This is the same formula as above, of course, but it
comes with an additional geometric interpretation. Suppose L2 = 4pA. It
follows that A = pr2. Now the region is completely contained
inside the circular disk. The only way for it to have the same area is
for it to be the circular disk! This formula, along with this
additional geometric interpretation, is known as a Bonnesen-type
isoperimetric inequality.
A similar proof that works in spherical and hyperbolic geometry is
contained in the paper Planimeters
and Isoperimetric Inequalities on Constant Curvature Surfaces.
In these spaces the isoperimetric inequality is
L2 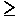 4pA -
kA2,
4pA -
kA2,
where k is the curvature of the space: k is
1/R2 for a sphere, k is
negative for the hyperbolic plane.
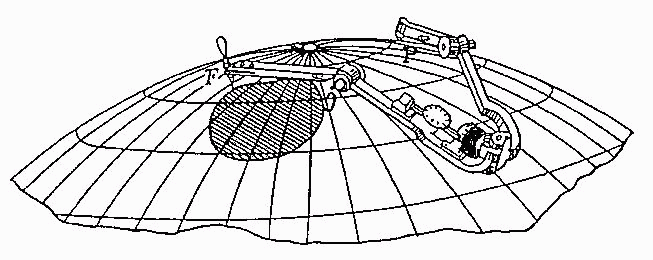
Spherical planimeter, Jacob Amsler, 1884
Two survey articles on isoperimetric inequalities by
R. Osserman:
Bulletin of the American Mathematical Society, Nov. 1978
American Mathematics Monthly, Jan. 1979
Main planimeter page
Robert Foote
26 May 2009

