|
|
|
| A | B |
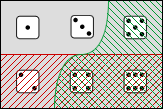
Fig. 5.2.1-1. Propositions expressed by two sentences (A) and an only-if-conditional (B) whose main clause leaves open the possibilities at the left in A.
The bare word if is not the only way of making a conditional claim. Compare the following forecasts:
It will rain tomorrow if the front moves through.
It will rain tomorrow only if the front moves through.
The first was our original example of hedging a claim with an if-clause. The second differs in the substitution of only if for if. This makes quite a difference, though, for the second does not hedge the claim that it will rain but instead puts up a fence around it by placing a limit on the cases in which it might be true. While the first conditional leaves open some possibilities its main clause rules out, the second rules out some possibilities that its main clause leaves open. A forecaster who asserts the second sentence is committed to it not raining in cases where the front does not move through. That is, the force of only if is to offer a limited denial of the main clause rather than a limited assertion of it.
These considerations suggest the table below for sentences of the form ψ only if φ, sentences we will speak of as only-if-conditionals. In cases where the condition φ holds, the claim cannot go wrong. The form ψ only if φ provides information only about cases where φ fails and, in these, its truth value is opposite that of ψ. Thus ψ only if φ is false only in a case where ψ is true even though φ is false. This is what makes it a limited denial of ψ; it rules out possibilities left open by ψ, but it rules out only those in which the condition φ does not hold. Or to put it in other terms, it limits the truth of ψ to cases where φ is true; it does not assert ψ in those cases but excludes it in others.
| φ | ψ | ψ | only if | φ |
| T | T | T | ||
| T | F | T | ||
| F | T | F | ||
| F | F | T |
Diagrams of propositions may be of some help here, too. Figure 5.2.1-1 should be compared to Figure 5.1.2-1 and also to Figure 3.1.2-1. In the example we have been using, 5.2.1-1B represents the proposition expressed by The number shown by the die is less than 4 only if it is odd.

|

|
|
| A | B |
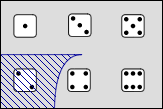
Fig. 5.2.1-1. Propositions expressed by two sentences (A) and an only-if-conditional (B) whose main clause leaves open the possibilities at the left in A.
Like the if-conditional, the only-if-conditional is a weak claim, leaving open possibilities in three of the four regions shown in Figure 5.2.1-1A; but it narrows the possibilities left open by the main clause (the area at the left in 5.2.1-1A) to those also left open by the subordinate clause. This is the reason for saying the function of an only-if-conditional is to fence in. Comparison with Figure 2.1.1-1 shows that it provides exactly the further information needed to move from the possibilities left open by the main clause ψ to the narrower range left open by ψ ∧ φ.
We will not introduce a new symbol for the connective marked by only if. A claim of the form ψ only if φ can be seen as a claim ¬ ψ hedged to be conditional on the truth of ¬ φ; and that means we can express ψ only if φ as ¬ ψ ← ¬ φ. (You should check that this form has the correct table.)
While only if raises most of the same issues if, these arise with different severity and in different ways. For example, it is possible to move an only-if-clause to the front of a sentence, but this is done only in rather formal contexts. You would not expect a television weather forecaster to use the sentence Only if the front moves through will we have rain tomorrow. There are only-if-conditionals in the subjunctive that we must leave unanalyzed (for example, We would be able to see the eclipse only if we were near the equator) but they are less common than subjunctive if-conditionals.