|
| |
| A | B |
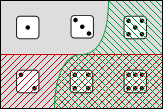
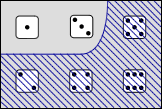
Fig. 2.1.1-1. Propositions expressed by two sentences (A) and their conjunction (B).
We are interested in logical forms as a way of stating general laws of entailment. Let us begin by looking at cases of entailment that seem to involve the word and. Here is an example:
That bear is large and edgy ⇒ That bear is large
In attempting to understand any fact, it is useful to collect related facts. One way to search for related facts about entailment is to look for cases involving sentences similar in grammatical form to those above. If we follow this route, we run into entailments like this:
That car is cheap and reliable ⇒ That car is cheap
And we will eventually hit upon a general pattern like this:
a is P and Q ⇒ a is P.
If we look a little farther afield, we also find examples like
It was hot and there was a storm before dark ⇒ It was hot,
which follows the pattern
φ and ψ ⇒ φ.
This pattern can be seen to operate also in examples of the first group if we paraphrase them, transforming
That bear is large and edgy,
for instance, into
That bear is large and that bear is edgy.
In applying a pattern by first paraphrasing, we treat a sentence as having a form that is hidden by its surface appearance. Much of our analysis of logical form will involve this sort of transition.
Assuming we are willing to apply the second pattern by way of a paraphrase, we have a fairly general law of inference in which the word and plays a key role. If we look at what this role entails, we see that and marks a particular sort of compound sentence formed of component sentences, one that we will label a conjunction. So the word and is a sign for an operation that forms conjunctions. We will call an operation that forms compound sentences out of component sentences a connective, and we will refer to the connective we are considering here as conjunction, marking it with the sign ∧ (one of whose names is logical and). (The use of the term conjunction for both the operation of conjoining and the compound that results may seem confusing, but it follows a pattern that is used fairly often in English—as when the word distribution is used for both the act of distributing and its result.) It will often be convenient to employ a further related term and refer to the components of a conjunction as its conjuncts.
Using these ideas, we can express our analysis of That bear is large and edgy as
That bear is large ∧ that bear is edgy,
and we can express our principle of entailment as
φ ∧ ψ ⇒ φ.
This symbolic notation can save space but it is often convenient to use English to mark conjunction. When we do this, we will use the construction both ... and ... and write it (as done here) using a special type. So the principle above could be stated as
both φ and ψ ⇒ φ.
(The reason for using the particle both in addition to and will be discussed later.)
At this point, we have reached a stage like that reached by a physicist who recognizes pressure, temperature, and volume as physical quantities and has formulated a law relating them but who does not know why the law holds. That is, we have a generalization about entailment that we can apply in special cases, but we cannot say why this generalization is true. What is it about conjunction that makes this sort of entailment work?
We can find an answer by again scaring up some more facts. Notice, for example, that the entailment that got us started is matched by a second.
That bear is large and edgy ⇒ That bear is edgy.
Moreover, we can see not only that the sentence That bear is large and edgy entails each of the two sentences That bear is large and That bear is edgy but also that it is entailed in turn by the two taken together. If we abbreviate the longer sentence by B and the two shorter sentences as L and N, respectively, we have collected the following facts:
B ⇒ L
B ⇒ N
L, N ⇒ B
And checking other cases of conjunction would show us that these are instances of three general laws.
φ ∧ ψ ⇒ φ
φ ∧ ψ ⇒ ψ
φ, ψ ⇒ φ ∧ ψ.
Or, using English to express the forms,
both φ and ψ ⇒ φ
both φ and ψ ⇒ ψ
φ, ψ ⇒ both φ and ψ.
So far, all we have done is to accumulate more general laws, but it is often easier to understand a larger number of facts because a pattern can begin to emerge.
We can begin to provide a single account of these laws by recalling our definition of entailment. In positive form, it says that a set Γ entails a sentence φ if and only if φ is T in every possible world in which each member of Γ is T. Restating our three laws in these terms, we have
In short, φ ∧ ψ is true in a possible world if and only if both φ and ψ are true. This means that the truth value of the compound φ ∧ ψ is determined by the truth values of the components φ and ψ, a fact we can express in the truth table below.
| φ | ψ | φ | ∧ | ψ |
| T | T | T | ||
| T | F | F | ||
| F | T | F | ||
| F | F | F |
This table shows the contribution of conjunction to the truth conditions of compound sentences formed using it, for it tells us how to determine the truth value of a conjunction φ ∧ ψ in any possible world once we know the truth values of the conjuncts φ and ψ. And the table also shows what lies behind the general laws of entailment that led us to it: it is because conjunction makes this sort of contribution to the meaning of sentences that those laws hold. A particular way of associating an output truth value with input truth values is a truth function, so we can say that conjunction expresses a truth function, and we can say the laws of entailment stated above reflect the character of the truth function that conjunction expresses.
It is worth pausing a moment to look at the way in which the proposition that is expressed by a conjunction is related to the propositions that are expressed by its components. Since a conjunction is false whenever either component is false, it rules out any possibility ruled out by either component; and, since the possibilities ruled out are an indication of the information a sentence contains, we can say that a conjunction contains all the information contained in its components. This means that the effect of conjunction is to add up informational content. Now, more information means fewer possibilities left open and, looking at the table in these terms, we see that a conjunction leaves open only the possibilities left open by both components. The range of possibilities it leaves open is the region in the full space of possibilities where the ranges of possibilities left open by the two components overlap.
For example, the sentence The number shown by the die is odd and less than 4 can be analyzed as the conjunction The number shown by the die is odd ∧ the number shown by the die is less than 4. The first component rules out possibilities where the die shows 2, 4, or 6 and the second rules out possibilities where it shows 4, 5, or 6. The conjunction rules out all these possibilities—that is, any possibility where the die shows 2, 4, 5, or 6. Looking at things in terms of the possibilities left open, the first component leaves open those where the die shows 1, 3, or 5 and the second leaves open those where it shows 1, 2, or 3. The conjunction leaves open a possibility when it is left open by both components; that is, it leaves open those where the die shows 1 or 3.
This is shown pictorially in Figure 2.1.1-1 below.

|

| |
| A | B |
Fig. 2.1.1-1. Propositions expressed by two sentences (A) and their conjunction (B).
Here, each rectangle represents the space of all possible worlds. The die faces mark regions consisting of the possible worlds in which the die shows one or another number. In Figure 2.1.1-1A, the possibilities ruled out by the first component are at the bottom in the region hatched in red from lower left to upper right while those ruled out by the second component occupy the region at the right hatched in green from upper left to lower right. The possibilities left open by the first component then form the region at the top outside the red hatching while those left open by the second are in the region at the left outside the green hatching. Figure 2.1.1-1B shows the proposition expressed by the conjunction of these two sentences. The possibilities ruled out add up to form the region hatched in blue; those left open are in the unhatched region at the top left where the ranges of possibilities left open by the original components overlap. These diagrams can be compared to the truth table for conjunction. The sort of worlds covered by first row of the table, worlds where both components are true, appear at the top left of the 2.1.1-1A; the other rows of the table correspond to the remaining three regions of the this diagram—those at the top right, the bottom left, and the bottom right, respectively.