These are selections from a textbook and are sufficiently self-explanatory that I won’t offer comments on them. Instead I’ll supplement Giere’s discussion with some notes on numerical confirmation via a law of probability known as “Bayes’ theorem.” You should focus your reading on Giere—in the two components assigned for Mon. and Wed., respectively—and then look over these notes if you have time. Our class discussion will begin with Giere and I’ll turn to Bayes’ theorem only if we have time available.
The theory of probability
Let us call whatever it is that probabilities are assigned to “events.” The theory of probability applies to a range of events that includes all events derived in certain ways from others. First of all, we want to have an event U (for “universal”) that happens no matter what event occurs. We also want to have, for any events E and F, further events not-E (which happens when E does not), E or F (which happens when at least one of E and F does) and E and F (which happens when both of E and F do). In many cases, it is also necessary to have events E1 or E2 or … and E1 and E2 and … for any series of events E1, E2, ….
There are then only a few basic axioms assumed for probability.
(i) prob(E) ≥ 0 for any event E;
(ii) prob(U) = 1;
(iii) if E and F mutually exclusive, then prob(E or F) = prob(E) + prob(F); or, more generally, if every pair of events from E1, E2, … are mutually exclusive, then prob(E1 or E2 or …) is the sum of the probabilities prob(E1), prob(E2), …. (Events E and F are mutually exclusive when they cannot occur together—i.e., when not-(E and F) = U.)
These axioms say (i) that probabilities are never negative, (ii) that the probability of the universal event U is 1, and (iii) that probabilities of mutually exclusive alternatives can be added to give the probability that at least one of them holds. Many other facts follow from these. For example, logic tells us that E or not-E = U and that E and not-E are mutually exclusive. It follows for any event E that prob(E) + prob(not-E) = 1, that prob(not-E) = 1 - prob(E), and that prob(E) ≤ 1.
Since the assumptions above are enough to get the usual laws of probability, they are all that need to be satisfied by an idea in order for it to count as an interpretation of probability theory. Of course, that’s not to say that any way of satisfying them counts as a sensible concept of probability.
Bayes’ theorem
One of the basic principles of probability theory that is most useful in applications to induction is an idea due to the 18th century clergyman Thomas Bayes (1702-1761). To state it we need the idea of conditional probability, the probability of one event given that another occurs. It is defined as follows:
prob(E given F) = prob(E and F) / prob(F)
which makes sense only if prob(F) > 0. Conditional probability is a quantity assigned to a pair of events that gives the probability of the first relative to the second. For example, prob(The die is even given The die is 1, 2, or 3) = 1/3 but prob(The die is even given The die is 4, 5, or 6) = 2/3.
Multiplying both sides of the definition of conditional probability by prob(F) gives the usual formula for the probability of a conjunctive event:
prob(E and F) = prob(E given F) × prob(F)
Applying this to the event H and E = E and H and dividing both sides by prob(E)—so we assume prob(E) > 0—gives one form of Bayes’ Theorem:
prob(H given E) = prob(E given H)prob(E) × prob(H)
The letters here reflect the chief application of the idea to induction: H is a hypothesis and E is the statement of some evidence. The quantity on the left, prob(H given E), is the probability of a hypothesis H given evidence E (its “posterior probability”), and the quantity on the far right, prob(H), is the probability that the hypothesis would have without considering the evidence (its “prior probability”). The factor that converts the prior into the posterior probability is the ratio of the probability prob(E given H) of the evidence given the hypothesis (the probability with which the hypothesis would lead us to predict the evidence) and the probability prob(E) that the evidence would have if we make no assumptions about the truth of the hypothesis.
It is natural to say that evidence confirms a hypothesis when the posterior probability of the hypothesis is greater than its prior probability. Notice that this happens to the extent that the hypothesis makes the evidence more likely than it would be if the hypothesis was not assumed. A hypothesis is best confirmed when the evidence is surprising—i.e., where prob(E) is small—but is strongly predicted by the hypothesis—i.e., where prob(E given H) is large. (We will return these ideas below.)
The quantities on the right in Bayes’ theorem are not all independent, so you cannot freely choose any values from 0 to 1 for each of these probabilities. When prob(H) < 1 and prob(E given not-H) > 0, Bayes’ theorem can be put into a another form which does not have this limitation. If we divide each side of Bayes’ theorem above by the two sides of the corresponding principle for not-H, we get
prob(H given E)prob(not-H given E) = prob(E given H)prob(E given not-H) × prob(H)prob(not-H)
The expression at the far right is a formula for the odds on H (e.g., the odds on something whose probability is .75 are .75/.25 = 3/1—or 3 to 1 odds), and the expression at the far left can be thought of as a formula for conditional odds. So we can rewrite this formula as
odds(H given E) = prob(E given H)prob(E given not-H) × odds(H)
The quantity in the middle is sometimes called the “likelihood ratio” for given evidence, so this form of Bayes’ theorem can be expressed by saying that the posterior odds on a hypothesis are equal to the product of the prior odds and the likelihood ratio. All three probabilities on the right can be assigned independently, so the posterior odds (and therefore probability) can be thought of as a function of three things, the prior probability (which determines the prior odds), the strength with which the hypothesis predicts the evidence, and the extent to which the evidence would be expected if the hypothesis were false. The first two factors increase the posterior probability of the hypothesis while the third decreases it.
Of course, we cannot say that the posterior probability is a product of the prior probability and the likelihood ratio because a large increase in odds need not be a large increase in probability (e.g., doubling odds of 50 to 1 to 100 to 1 takes you from a probability a little over .98 to one a little over .99). The diagram below is intended to give a you a sense of the actual effects on probabilities of various likelihood ratios.
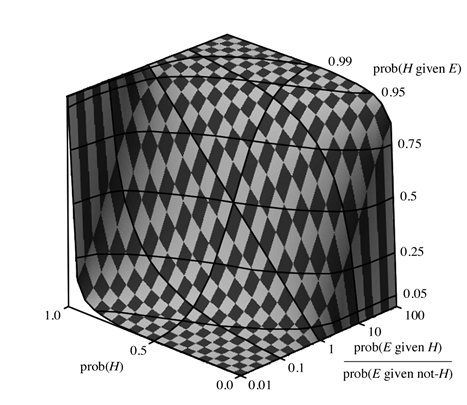
The posterior probability is the vertical axis. The likelihood ratio is shown in a logarithmic scale running from 1/100 to 100 on the axis running into the picture to the right. The prior probabilities are on the axis running into the picture on the left. Notice that when the likelihood ratio is 1, the prior and posterior probabilities are the same (the straight line running through the middle of the surface). When the likelihood ratio is greater than 1, the increase in low prior probabilities is roughly the likelihood ratio but the increase in high prior probabilities is much less. The situation is reversed when the likelihood ratio is less than 1 (and the evidence disconfirms the hypothesis). If you would like to experiment with numerical values for these quantities the course web site has an on-line calculator (phi272Bayescalc1) that will do the arithmetic for you.
Bayes’ theorem and confirmation
One of the values of Bayes’ theorem for thinking about the confirmation of hypotheses is that it distinguishes three sorts of factors that may play a role in confirmation. And it is possible to classify many of the factors that are known to play a role in confirmation in this way. Here are three examples.
• Evidence that confirms each of two hypotheses is often thought to confirm the simpler of the two hypotheses more strongly. Simplicity is an internal feature of a hypothesis, a feature it has independent of evidence, so it is the sort of thing that be reflected by the prior probability prob(H).
• The ideal sort of evidence for confirming a hypothesis is evidence whose failure would falsify it. This is evidence for which prob(E given H) = 1 because, for such evidence, prob(not-E given H) = 0 and therefore prob(H given not-E) = 0. And evidence for which prob(E given H) = 1 makes the likelihood ratio as large as possible, so Bayes’ theorem agrees that this is the best evidence. Criticisms of Popper’s falsificationism suggest such evidence may be hard to come by—i.e., it hard to rule out a hypothesis absolutely—but Bayes’ theorem tells us that any evidence for which prob(E given H) is close to 1 would be almost as good. And, in general, Bayes’ theorem says that a hypothesis will be better supported by evidence that it predicts with greater confidence.
• It is often said that variety in evidence is more valuable than an increased quantity of the same evidence. It can be a little hard to define the notion of “variety” used here since any new evidence is different from earlier evidence in some respect (the time at which it is obtained if nothing else). But Bayes’ theorem suggests a way in which some sorts of variety might be significant. As observations of a given sort start to follow a pattern, we are likely to expect that pattern to be repeated even when a general hypothesis predicting it is false: if we have seen many white swans, we might expect the next one we see to be white even if we assume that not all swans are white. As a result, we would expect the quantity prob(E given not-H) to increase as we begin to see a pattern in the evidence. Further evidence of the same sort would then do less to confirm the hypothesis than it did when prob(E given not-H) was smaller, and turning to evidence of a different sort might return us to lower values for prob(E given not-H).
Use of Bayes’ theorem in confirmation is generally tied to a natural rule for updating probabilities in response to new evidence. Let us say that the probabilities we assign at any given time are relative to the sum total K of our knowledge at that time and write this assignment as “probK.” When we obtain new evidence E our knowledge changes from K to K and E and our probability assignment from probK to probK and E. The rule for altering probabilities on the basis of new evidence then requires that
probK and E(F) = probK(F given E)
for any event F. Bayes’ theorem then provides a way of calculating the quantity on the right. Putting it together with the rule above, we get the following rules for probabilities and for odds:
probK and E(F) = probK(E given F)probK(E) × probK(F)
oddsK and E(F) = probK(E given F)probK(E given not-F) × oddsK(F)
for any event F. In particular, the second rule tells us that we should alter our probability assignments on the basis of new evidence by way of the likelihood ratios for that evidence.
If you would like to look at confirmation numerically, the course web site has an on-line calculator (phi272Bayescalc2) that will carry out repeated updates in the context of enumerative induction (i.e., confirmation of a hypothesis of the form All S are P on the basis of particular instances of it).