Phi 272 F06, reading guide

Reading guide for Tues 9/5: Carnap, An Introduction to the Philosophy of Science,
ch. 3, pp. 29-39.

Chapter 3 focuses on the idea of logical probability, which Carnap sees as the sense of probability we use when we speak of the probability of conclusion given certain premises or the probability of a hypothesis given certain evidence. His discussion is mainly historical and somewhat defensive. In the time since this was written, more attention have been given to the views of the people he discusses, but this is due less to an interest in the logical probability as Carnap understands it than it is to a rise of interest in fourth interpretation of probability theory we will consider, subjective probability.

Subjective probability is an interpretation of probability theory as being concerned with degrees of belief. The laws of probability function as constraints on the rationality of our degrees of belief. In particular, unless our degrees of belief obey these laws, we are liable to accept bets that would lead us to lose money no matter what the outcome. Probability in this sense is still subjective because different degrees of belief in a given claim are consistent with the laws of probability (since many different probabilities are). However, the effect of this subjectivity is moderated by laws of probability that can bring people’s degrees of belief closer together as they experience the same evidence.

Applications of both logical probability and subjective probability make extensive use of Bayes’ theorem (see below), which provides a principle for calculating the way the probability of a hypothesis given certain evidence depends on its probability independent of the evidence (its “prior probability”). This provides the basis for instructions for modifying one’s degrees of belief in response to evidence. Of course, the result depends not only on the evidence (and the probability assigned to it) but also on the prior probability of the hypothesis. Logical probability is now typically understood as an attempt to specify prior probabilities on logical grounds. Subjective probability does not attempt to constrain them in this way but relies instead on impact of shared evidence.

Carnap’s idea that confirmation by evidence can be assigned a degree measurable by logical probability is not the only controversial aspect of his views. Karl Popper (who was mentioned as a proponent of the idea of propensities) held that science should be concerned not with confirmation but instead with falsification, with rejecting false hypotheses rather than supporting true ones.

He associated an emphasis on confirmation with a tendency to try to preserve hypotheses by adding qualifications and modifications in response to conflicting evidence. He thought a scientist should instead formulate the simplest and boldest hypothesis consistent with available evidence and then try to falsify it. A hypothesis that survived attempts to falsify it acquired a kind of support that he called “corroboration,” but this is not just a different word for probability because, he insisted, the best corroborated hypotheses were not the most likely to be true. That is because a hypothesis would be better corroborated the more severe the testing it had under gone; and, other things being equal, it is the bolder and less probable hypothesis that is more severely tested.

He suggested that the idea that science should focus on confirmation was associated with a view of the acquisition of knowledge that focused on the collection of facts and saw generalizations as a product of this collection. He called this the “bucket” model of science and contrasted it with a “searchlight” model according to which knowledge developed by formation of conjectures, followed by investigation in the direction they suggested. The trial-and-error pattern of repeated conjecture and refutation is something he did not limit to scientific knowledge but saw in the development of all human knowledge and something he linked more broadly still to the process of natural selection.

One of the things you should do in preparation for discussion is to think whether you take confirmation or falsification to be more central to the aim of science. Although Popper agreed with Carnap and the logical positivists on many issues, he and his followers were clearly divided on this issue from people sympathetic the views of philosophers like Carnap, Reichenbach, and Hempel. And the issue is important enough that it is natural to see the philosophy of science in the decades just following WWII as divided into two schools along these lines. You can find a selection of quotations from Popper on these topics at the end of this reading guide.

Let us call whatever probabilities are assigned to “events.” The theory of probability begins with the assumption of a range of events that includes all events specified in certain ways relative to others. In particular, we want to have an event U that happens no matter what event occurs and to have, for any events E and F, further events not-E (which happens when E does not), E or F (which happens when at least one of E and F does) and E and F (which happens when at both of E and F do). In many cases also, it is necessary to have events E₁ or E₂ or … and E₁ and E₂ and … for any series of events E₁, E₂, ….

(i) prob(E) ≥ 0 for any event E;

(ii) prob(U) = 1;

(iii) if E and F mutually exclusive, then prob(E or F) = prob(E) + prob(F); or, more generally, if every pair of events from E₁, E₂, … are mutually exclusive, then prob(E₁ or E₂ or …) is the sum of the probabilities prob(E₁), prob(E₂), ….

(Events E and F are mutually exclusive when they cannot occur together—i.e., when not-(E and F) = U.)

These assumptions are enough to get the usual laws of probability, and they are all that need to be satisfied in order to have an interpretation of probability theory. Of course, that’s not to say that any way of satisfying them counts as a sensible concept of probability.

One of the basic principles of probability theory that is most useful in applications to induction is an idea due to the 18^th century clergyman Thomas Bayes (1702-1761). To state it we need the idea of conditional probability, the probability of one event given that another occurs. It is defined as follows:

which makes sense only if prob(F) > 0. (The conditional probability is not the probability of some new sort of event “E given F” but instead a quantity assigned to a pair of events.) Multiplying both sides by prob(F) gives the usual formula for the probability of conjunctive event:

Applying this to the event H and E = E and H and dividing both sides by prob(E) gives Bayes’ Theorem:

The letters here reflect the chief application of the idea to induction: the probability of a hypothesis H given evidence E (its “posterior probability”) is the product of the probability prob(H) that the hypothesis would have independent of the evidence (its “prior probability”) and the ratio of the probability of the evidence given the hypothesis (the probability with which the hypothesis would lead us to predict the evidence) and the probability prob(E) that the evidence would have if we make no assumptions about the truth of the hypothesis.

It is natural to say that evidence confirms a hypothesis when the posterior probability of the hypothesis is greater than its prior probability. Notice that this happens to the extent that the hypothesis makes the evidence more likely than it would be anyway. In short a hypothesis is best confirmed by a surprising event that it strongly predicts.

The quantities on the right in Bayes’ theorem are not all independent, so you cannot freely choose any values from 0 to 1 for each of these probabilities. When prob(H) < 1, Bayes’ theorem can be put into a another form which does not have this limitation. If we divide each side of Bayes’ theorem above by the two sides of the corresponding principle for not-H, we get

prob(H given E)prob(not-H given E) = prob(E given H)prob(E given not-H) × prob(H)prob(not-H)

The expression at the right is a formula for the odds on H (e.g., the odds on something whose probability is .75 are .75/.25 = 3/1 or 3 to 1 odds), and the expression at the left can be thought of as a formula for conditional odds. So we can write this as

odds(H given E) = prob(E given H)prob(E given not-H) × odds(H)

The quantity in the middle is sometimes called the “likelihood ratio” for given evidence, so this form of Bayes’ theorem can be expressed by saying that the posterior odds on a hypothesis are equal to the product of the prior odds and the likelihood ratio. All three numbers on the right can be assigned independently, so the posterior odds (and therefore probability) can be thought of as a function of three things, the prior probability (which determines the prior odds), the strength with which the hypothesis predicts the evidence, and the extent to which the evidence would be expected if the hypothesis were false. The first two factors increase the posterior probability of the hypothesis while the third decreases it.

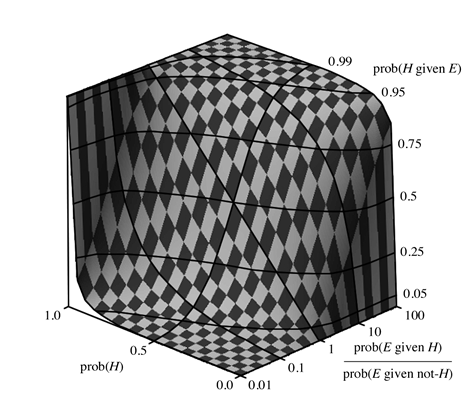
Of course, we cannot say that the posterior probability is a product of the prior probability and the likelihood ratio because a large increase in odds need not be a large increase in probability (e.g., doubling odds of 50 to 1 takes you from a probability a little over .98 to one a little over .99). The following diagram is intended to give a you a sense of the actual effects on probabilities of various likelihood ratios.

The posterior probability is the vertical axis. The likelihood ratio is shown in a logarithmic scale running from 1/100 to 100 on the axis running into the picture to the right. The prior probabilities are on the axis running into the picture on the left. Notice that when the likelihood ratio is 1, the prior and posterior probabilities are the same (the straight line running through the middle of the surface). When the likelihood ratio is greater than 1, the increase in low prior probabilities is roughly the likelihood ratio but the increase in high prior probabilities is much less. The situation is reversed when the likelihood ratio is less than 1 (and the evidence disconfirms the hypothesis).

Selections from: Karl Popper, Unended Quest: an Intellectual Autobiography (La Salle, Ill.: Open Court, 1982).

… I could apply my results concerning the method of trial and error in such a way as to replace the whole inductive methodology by a deductive one. The falsification or refutation of theories through the falsification or refutation of the their deductive consequences was, clearly, a deductive inference (modus tollens). The view implied that scientific theories, if they are not falsified, for ever remain hypotheses or conjectures.

Thus the whole problem of scientific method cleared itself up, and with it the problem of scientific progress. Progress consisted in moving towards theories which tell us more and more—theories of ever greater content. But the more a theory says the more it excludes or forbids, and the greater are the opportunities for falsifying it. So a theory with greater content is one which can be more severely tested. This consideration led to a theory in which scientific progress turned out not to consist in the accumulation of observations but in the overthrow of less good theories and their replacement by better ones, in particular by theories of greater content.…

… There is no induction, because universal theories are not deducible from singular statements. But they may be refuted by singular statements, since they may clash with descriptions of observable facts.

Moreover, we may speak of “better” and of “worse” theories in an objective sense even before our theories are put to the test: the better theories are those with the greater content and the greater explanatory power (both relative to the problems we are trying to solve). And these, I showed, are also the better testable theories; and—if they stand up to tests—the better tested theories.

This solution of the problem of induction gives rise to a new theory of the method of science, to an analysis of the critical method, the method of trial and error: the method of proposing bold hypotheses, and exposing them to the severest criticism, in order to detect where we have erred.

From the point of view of this methodology, we start our investigation with problems. We always find ourselves in a certain problem situation; and we choose a problem which we hope we may be able to solve. The solution, always tentative, consists in a theory, a hypothesis, a conjecture. The various competing theories are compared and critically discussed, in order to detect their shortcomings; and the always changing, always inconclusive results of the critical discussion constitute what may be called “the science of the day.”

Thus there is no induction: we never argue from facts to theories, unless by way of refutation or “falsification.” This view of science may be described as selective, as Darwinian. By contrast, theories of method which assert that we proceed by induction or which stress verification (rather than falsification) are typically Lamarckian: they stress instruction by the environment rather than selection by the environment.

As for my degree of corroboration, the idea was to sum up, in a short formula, a report of the manner in which a theory has passed—or not passed—its tests, including an evaluation of the severity of the tests: only tests undertaken in a critical spirit—attempted refutations—should count. By passing such tests, a theory may “prove its mettle”—its “fitness to survive.” Of course, it can only prove its “fitness” to survive those tests which it did survive; just as in the case of an organism, “fitness,” unfortunately, only means actual survival, and past performance in no way ensures future success.

A decisive point about degree of corroboration was that, because it increased with the severity of tests, it could be high only for theories with a high degree of testability or content. But this meant that degree of corroboration was linked to improbability rather than to probability: it was thus impossible to identify it with probability….

Selections from: Karl Popper, “The Bucket and the Searchlight: Two Theories of Knowledge,” an appendix to Objective Knowledge: an Evolutionary Approach (Oxford: Oxford University Press, 1975).

According to [the bucket theory], our mind resembles a container—a kind of bucket—in which perceptions and knowledge accumulate. (Bacon speaks of perceptions as ‘grapes, ripe and in season’ which have to be gathered, patiently and industriously, and from which, if pressed, the pure wine of knowledge will flow.)

Strict empiricists advise us to interfere as little as possible with this process of accumulating knowledge. True knowledge is pure knowledge, uncontaminated by those prejudices which we are only too prone to add to, and mix with, our perceptions; these alone constitute experience pure and simple. The result of these additions, of our disturbing and interfering with the process of accumulating knowledge, is error. Kant opposes this theory: he denies that perceptions are ever pure, and asserts that our experience is the result of a process of assimilation and transformation—the combined product of sense perceptions and of certain ingredients added by our minds. The perceptions are the raw material, as it were, which flows from outside into the bucket, where it undergoes some (automatic) processing—something akin to digestion, or perhaps to systematic classification—in order to be turned in the end into something not so very different from Bacon’s ‘pure wine of experience’; let us say, perhaps, into fermented wine.

I do not think that either of these views suggests anything like an adequate picture of what I believe to be the actual process of acquiring experience, or the actual method used in research or discovery.…

In science it is observation rather than perception which plays the decisive part. But observation is a process in which we play an intensely active part. An observation is a perception, but one which is planned and prepared.… We can assert that every observation is preceded by a problem, a hypothesis (or whatever we may call it); at any rate by something that interests us, by something theoretical or speculative. This is why observations are always selective, and why they presuppose something like a principle of selection.

All this applies, more especially, to the formation of scientific hypotheses. For we learn only from our hypotheses what kind of observations we ought to make: whereto we ought to direct our attention; wherein to take an interest. Thus it is the hypothesis which becomes our guide, and which leads us to new observational results.

This is the view which I have called the ‘searchlight theory’ (in contradistinction to the ‘bucket theory’). [According to the searchlight theory, observations are secondary to hypotheses.] Observations play, however, an important role as tests which a hypothesis must undergo in the course of our [critical] examination of it. If the hypothesis does not pass the examination, if it is falsified by our observations, then we have to look around for a new hypothesis. In this case the new hypothesis will come after those observations which led to the falsification or rejection of the old hypothesis. Yet what made the observations interesting and relevant and what altogether gave rise to our undertaking them in the first instance, was the earlier, the old [and now rejected] hypothesis.

… Science never starts from scratch; it can never be described as free from assumptions; for at every instant it presupposes a horizon of expectations—yesterday’s horizon of expectations, as it were. Today’s science is built upon yesterday’s science [and so it is the result of yesterday’s searchlight].…

… The horizon of expectations plays the part of a frame of reference: only their setting in this frame confers meaning or significance on our experiences, actions, and observations.

Observations, more especially, have a very peculiar function within this frame. They can, under certain circumstances, destroy even the frame itself; if they clash with certain of the expectations. In such a case they can have an effect upon our horizon of expectations like a bombshell. This bombshell may force us to reconstruct, or rebuild, our whole horizon of expectations; that is to say, we may have to correct our expectations and fit them together again into something like a consistent whole. We can say that in this way our horizon of expectations is raised to and reconstructed on a higher level, and that we reach in this way a new stage in the evolution of our experience; a stage in which those expectations which have not been hit by the bomb are somehow incorporated into the horizon, while those parts of the horizon which have suffered damage are repaired and rebuilt. This has to be done in such a manner that the damaging observations are no longer felt as disruptive, but are integrated with the rest of our expectations. If we succeed in this rebuilding, then we shall have created what is usually known as an explanation of those observed events [which created the disruption, the problem].