6.1.1. A richer grammar

While there are more truth-functional connectives that we might study and more questions we might ask about those we have studied, we will now move on from truth-functional logic. The logical forms we will turn to involve ways sentences may be constructed out of expressions that are not yet sentences. Although the kinds of expressions we will identify do not correspond directly to any of the usual parts of speech, our analyses will be comparable in detail to grammatical analyses of short sentences into words.

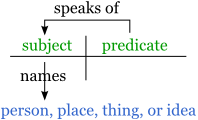
The simplest case of this sort of analysis is related to, but not identical with, the traditional grammatical analysis into subject and predicate. You might find a grammar text of an old-fashioned sort defining subject and predicate correlatively as the part of the sentence that is being spoken of and the part that says something about it. Of course, in saying that the subject is being spoken of, there would be no intention to say that the predicate is used to say something about words. So the text might go on to say that a subject contains a word that names the person, place, thing, or idea (to quote one of my high school grammar texts) about which something is being said. Thus we have the situation shown in Figure 6.1.1-1.

Fig. 6.1.1-1. The traditional picture of grammatical subjects and predicates.

This picture is really not adequate for either grammar or logic, but grammarians and logicians part company in the ways they refine it. Grammarians look for more satisfactory definitions of subject and predicate that capture, at least roughly, the expressions that have been traditionally labeled in this way. Logicians, on the other hand, accept something like the definitions above and look for expressions that really have the functions they describe, whether or not these expressions would traditionally be labeled subjects and predicates.

Subjects and predicates in the logical sense provide, along with sentences and connectives, examples of two broad syntactic categories, complete expressions and operations. Sentences are examples of complete expressions and connectives are examples of operations. Like connectives, operations in general can be thought of as expressions with blanks, expressions that are incomplete in the sense that they are waiting for input. We can classify operations according to the number and kinds of inputs they are waiting for and the kind of output they yield when they receive this input. In the case of connectives, both the input and the output consists of sentences.

A subject in the logical sense will be a kind of complete expression, an individual term. This is a type of expression whose function is to refer to something; it is an expression which can be described, roughly, as naming a person, place, thing, or idea. In 6.1.6, we will consider the full range of expressions that count as individual terms but, for now, it will be enough to have in mind two basic kinds of example—proper names (such as Socrates, Indianapolis, Hurricane Isabel, or 3) and simple definite descriptions formed from the definite article the and a common noun (such as the winner, the U.S. president, the park, the book, or the answer).

In the simplest case, a predicate in the logical sense—and this is what we will use the term predicate to speak of—is an expression that can be used to say something about the object referred to by an individual term. It is an operation whose input is an individual term and whose output is a sentence expressing what is said. Thus a logical predicate amounts to a sentence with a blank waiting to be filled by an individual term. In 6.1.2, we will move beyond this simple case to include predicates that require multiple inputs (i.e., that have several blanks to be filled). Such predicates are certainly not predicates in the grammatical sense; nonetheless a logical predicate will contain the main verb of any sentence it yields as output, so many of the simplest examples of predicates will correspond to verbs or verb phrases.

The categories of expressions we are working with now include the ones listed below (with simple examples in the style of some popular early elementary school readers from the mid-20^th century):

Since we now have a number of kinds of expression that might be input or output of an operation, there are many more sorts of operations that can be distinguished according to their input and output, and we will go on to consider some of them. For example, in 6.1.7, we will add a kind of operation which yields individual terms as output (for individual terms as input). The input and output of operations need not be limited to complete expressions, and in later chapters, we will add operations that take predicates as input.