|
|
|
| A | B |
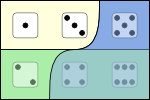
Fig. 5.2.3-1. Propositions expressed by two sentences (A) and an unless-conditional (B) whose main clause rules out the possibilities at the right in A.
5.2.3. Unless
Yet another sort of conditional appears in this example:
Here the speaker’s intent is to fence in the cases where the main clause fails (where they still have food), limiting its failure to the sort of situation described in the subordinate clause. The function of unless is thus closely related to the function of only if, and we could paraphrase the sentence above as
Like an only-if-conditional, an unless-conditional is automatically true in cases where the subordinate clause is true; but its truth value is the same as the main clause in cases where the subordinate clause is false. That is, the form ψ unless φ has the table below.
| φ | ψ | ψ | unless | φ |
| T | T | T | ||
| T | F | T | ||
| F | T | T | ||
| F | F | F |
This account of truth conditions appears also in Figure 5.2.3-1. Continuing the example of these diagrams, 5.2.3-1B represents the proposition expressed by The number shown by the die is less than 4 unless it is odd.

|

|
|
| A | B |
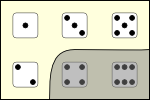
Fig. 5.2.3-1. Propositions expressed by two sentences (A) and an unless-conditional (B) whose main clause rules out the possibilities at the right in A.
There are two ways of describing the proposition on the right. First of all, it fences in the denial of the main clause. That is, it rules out some of the possibilities left open by the denial of the main clause ψ, those that are ruled out by the subordinate clause φ. This is to see the conditional as the proposition expressed by ¬ ψ only if φ. But the possibilities left open by the denial of the main clause are those ruled out by the main clause itself. So the conditional can be seen also to whittle down the possibilities ruled out by the main clause to those left open by the denial of the subordinate clause. And this is to see the conditional as the hedge of the main clause expressed by ψ if ¬ φ.
The same restatements appear if we trace our way back to if-conditionals in order to get a way of expressing this conditional symbolically. The form ψ unless φ amounts to ¬ ψ only if φ and we are treating the latter as ¬ ¬ ψ ← ¬ φ. If we use the principle of double negation to simplify this last expression, we get ψ ← ¬ φ as a rendering of ψ unless φ. The corresponding English paraphrase of ψ unless φ as ψ if it is not the case that φ is usually pretty good (good enough that if not is a common dictionary definition of unless).
There are enough steps in the path from unless to ← ¬ to justify a fear that the implicatures are not all in order when we arrive, but this account of unless works better than another symbolic representation that gives us the same table. Notice that, as far as truth conditions go, unless is a synonym for or. How far this synonymy goes beyond truth conditions can be seen by considering a few examples. We might paraphrase our example above as
and we would do so with reasonable success. But things do not work out as well in other cases, particularly with unless-conditionals concerning the future. The following two sentences have quite different implicatures:
Disjunction is not symmetric when it comes to an implicated connection between its two components, and we could paraphrase the first sentence better by We’ll either get to town soon or run out of gas, but the need to change the order of the clauses reduces the advantages of or over if not as a paraphrase of unless.
The remaining issues regarding unless pretty well parallel those concerning if and only if. It is possible to find an unless-clause at the front of a sentence (e.g., Unless we get to town soon, we’ll run out of gas). And the form ψ unless φ has, in addition to its core implicature that the truth of φ is necessary for the falsity of ψ, a secondary and easily canceled implicature of sufficiency. In our initial example (They have run out of food unless they received new supplies), this secondary implicature is rather weak if it is present at all, so there might be no need to add the canceling clause and they might have run out even if they got them. But, in other cases, the implicature is stronger. For example, in We’ll go unless it rains, we would have to add and we might go even if it does if we did not want to suggest that rain would be enough to keep us from going.