2.3.5. Presenting counterexamples
A dead-end open gap is always divided by an interpretation, and any interpretation that divides it also divides the ultimate argument of the derivation. We will finish off derivations that uncover invalidity by displaying this division. We will do that by exhibiting an interpretation that divides a dead-end open gap and calculating the truth values of the original premises and conclusions on that interpretation. In the example discussed in 2.3.1, this calculation is shown in the following table:
| A | B | C | (A | ∧ | ⊤) | ∧ | B | / | B | ∧ | (⊤ | ∧ | C) |
| T | T | F | | T | T | Ⓣ | | | | Ⓕ | T | F | |
Here the values of unanalyzed components have not been repeated on the right, but they are used to calculate the values of compounds containing them, with the order of calculation being guided by parentheses. In performing this calculation we are confirming that the interpretation dividing the gap really does constitute a counterexample to the ultimate argument; and we will say that, in constructing the table, we are presenting a counterexample. It will be our standard way of concluding the treatment of an argument whose derivation fails.
It is not always the case that all unanalyzed components of the ultimate argument all appear among the resources and goal of a dead-end gap. When unanalyzed components do not appear there, values must still be assigned to them in order for a truth value to be defined for each sentence in the ultimate argument; but it will not matter what value we assign to these further unanalyzed components. If an interpretation divides the gap, any way we choose to extend it to unanalyzed components not appearing in the gap’s proximate argument will still divide that gap and therefore divide the ultimate argument.
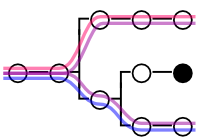
The example below is designed to illustrate this. Of the three interpretations shown, the first divides only the first dead-end gap (since it assigns the value T to the goal of the second dead-end gap), and the last divides only the second open gap (for a similar reason); but the middle one divides both open gaps. With 4 unanalyzed components, there are 2×2×2×2 = 24 = 16 possible interpretations, so there are 13 interpretations that do not divide either gap. The soundness and safety of our rules insures that the 3 interpretations shown above constitute counterexamples to the ultimate argument and that the other 13 do not.
| | | |
| │A ∧ B | 1 |
| ├─ | |
| 1 Ext | │A | |
| 1 Ext | │B | (4) |
| │ | |
| ││○ | A, B ⊭ C |
| │├─ | |
| ││C | 2 |
| │ | |
| │││● | |
| ││├─ | |
| 4 QED | │││B | 3 |
| ││ | |
| │││○ | A, B ⊭ D |
| ││├─ | |
| │││D | 3 |
| │├─ | |
| 3 Cnj | ││B ∧ D | 2 |
| ├─ | |
| 2 Cnj | │C ∧ (B ∧ D) | |
| A | B | C | D | A | ∧ | B | / | C | ∧ | (B | ∧ | D) | |
| T | T | F | T | | Ⓣ | | | | Ⓕ | | T | | divides first dead-end gap |
| T | T | F | F | | Ⓣ | | | | Ⓕ | | F | | divides both dead-end gaps |
| T | T | T | F | | Ⓣ | | | | Ⓕ | | F | | divides second dead-end gap |
While a dead-end gap is always divided by just one interpretation of the vocabulary appearing in its proximate argument, this interpretation may be provided by more than one interpretation of the derivation as a whole. That happens in both gaps here, and it also happens that a single interpretation of the whole derivation divides both of the gaps. That’s why we end up with 3 interpretations all told.
| A | B | C | D |
| T | T | F | T |
| T | T | F | F |
| T | T | T | F |
|
 |
|
Fig. 2.3.5-1. The interpretations dividing the dead-end gaps of the example above.
Since each of these interpretations divides all ancestors of the dead-end gap or gaps that it divides, any one of the three is enough to provide a counterexample to the ultimate argument. Beginning with chapter 6, it will prove to be most convenient to assign F to an unanalyzed component whenever we have a choice, and here that would lead us to the middle interpretation in the case of both gaps. But, for now, when an unanalyzed component does not appear in the proximate argument of a dead-end gap, the choice of the value to assign to it is entirely arbitrary.

