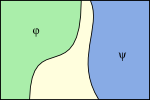
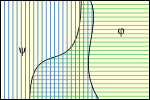
1.2.6. Contrasting content
We arrived at the relation of implication by considering entailment by a single premise. If we do the same with exclusion, we arrive at another relation between sentences. If φ excludes ψ, then the set {φ, ψ} formed of the two is inconsistent. When sentences φ and ψ are related in this way, it is equally true that ψ excludes φ. This reversability of this relation is reflected in the usual terminology for it: when there is no possible world in which φ and ψ are together true, φ and ψ are said to be mutually exclusive. There is no standard notation for the relation, and we will shortly have a way of expressing it in terms of entailment; but, when it is convenient to have special notation, we will write φ ▵ ψ to say that φ and ψ are mutually exclusive. This use of the up-pointing triangle is intended simply to reflect the shape of signs for some related ideas. One of these related ideas is Absurdity. In particular, notice that sentences φ and ψ are mutually exclusive if and only if they form an inconsistent set—that is, if they together entail ⊥.
Mutually exclusive sentences provide one example of the differences in propositions that made for the horizontal spread of the logical space of Figure 1.2.5-2. Indeed, one of the examples cited there, the sentences The package will arrive next Wednesday morning and The package will arrive next Wednesday afternoon was a pair of mutually exclusive sentences. Mutually exclusive sentences differ to the extent that there is no overlap in the possibilities they leave open. From one point of view, that is a pretty considerable difference; but, as the example illustrates, such sentences can still have a lot in common. And, in general, sentences that rule out many possibilities may express propositions that divide the space of possibilities in very similar ways even though they have no overlap in the ones they leave open.
Mutually exclusive sentences are opposed to one another, and they can be thought of as opposites. But there are different sorts of opposites. Some, like The glass is full and The glass is empty are extremes that may both fail in intermediate cases. Others, like The glass is full and The glass is not full cover all the ground between them and do not leave room for a third alternative. Opposites of the latter sort might be described as exactly opposite.
The difference between these sorts of opposition is tied to another way in which sentences can differ. Sentences φ and ψ are jointly exhaustive when there is no possible world in which both are false, when there is no possible world that both rule out. If we put together the possibilities left open by such sentences, the result will include all possibilities because any possibility ruled out by one must be left open by the other; and, in this sense, these sentences jointly exhaust all possibilities. Such sentences certainly differ in meaning—since there is no overlap in the possibilities they rule out, they can be said to have no common content—but they are not opposites in the sense of being incompatible. They might be thought of instead as complementary since, in regard to possibilities left open, each picks up where the other leaves off. We will use a down-pointing triangle ▿ as our notation for this relation, as in the case of ▵ because of the similarity in shape between ▿ and some ideas related to joint exhaustiveness. (Tautology is one of these ideas but we will not consider the relation between it and joint exhaustiveness until 1.4.)
When sentences are not only mutually exclusive but also jointly exhaustive, they are opposed in the second way described above: since they cannot both be false, one or the other is bound to hold and there is no room for a third alternative and they are exactly opposite. We will say that two sentences for which this is so are contradictory. Contradictory sentences—like The glass is full and The glass is not full—are bound to have opposite truth values. We will write φ ⋈ ψ to say that φ and ψ are contradictory (using the symbol bowtie). (You might think of the symbol as indicating that things get turned upside down when moving from one sentence to the other.)
Although our use of the term contradictory is the standard one in discussions of deductive logic, in ordinary speech this term is often applied to sentences that are only mutually exclusive. In particular, when a claim is said to be self-contradictory,
what is meant is that part of what it says excludes something else it says. Such a sentence will not contradict itself in the sense in which we will use the term because that would require that it be both true and false in each possible world, and that cannot happen if there are any possible worlds at all (an assumption we can feel safe in making).
Just as the propositions expressed by logically strong sentences need not be far different even when they are mutually exclusive, the propositions expressed by logically weak sentences need not be far different even when they are jointly exhaustive. It is contradictory sentences that provide the true extreme examples of difference. When logical space in Figure 1.2.5-2 is thought of in three dimensions, the contradictory sentences appear in diametically opposite positions. Notice that mutually exclusive sentences cannot both appear above the middle level (for such sentences leave open more than half the possibilities), and jointly exhaustive sentences cannot appear both below the middle. Contradictory sentences fall under both restrictions. A pair of contradictory sentences might both appear on the middle level, but it is also possible for one to be of more than average logical strength if the other is relatively weak. The extreme case of this is provided by ⊥ and ⊤, which are contradictory and constitute the only example of a contradictory pair the first of whose members implies the second.
The four basic deductive relations between two sentences that we have considered are shown in the following table:
| Relation | pattern ruled out |
| φ implies ψ (φ ⊨ ψ) | φ is T | ψ is F |
| φ is implied by ψ (ψ ⊨ φ) | φ is F | ψ is T |
| φ and ψ are mutually exclusive (φ ▵ ψ) | φ is T | ψ is T |
| φ and ψ are jointly exhaustive (φ ▿ ψ) | φ is F | ψ is F |
These are the only relations that can be defined by ruling out a specific pattern of truth values for two sentences because there are only four such patterns. Ruling out more than one pattern does not give us any relations beyond those already discussed. If we rule out the first two patterns, we are saying that the sentences are equivalent, and if we rule out the last two patterns, we are saying that they are contradictory. If we were to rule out any other pair of patterns, we would simply rule out a truth value for one of the sentences in all possible worlds, so we would be saying of this sentence that it was tautologous or that it was absurd. And that meas we would be describing a property of a single sentence rather than a relation between sentences. And ruling out three patterns would leave just one pattern and would specify the truth values of both sentences, saying of each them that it was tautologous or absurd. So, in one sense, the six relations for which we have terminology are the only ones possible.
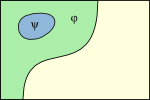
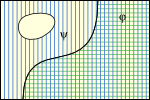
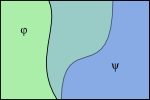
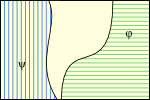
Relations between the propositions expressed by a pair of sentences can be depicted by relations of areas in logical space. The regions ruled out are shown shaded in the left column in Figure 1.2.6-1, and the regions left open are shown hatched in the right column.
Fig. 1.2.6-1. Three relations between sentences φ and ψ. (a, d) φ implies ψ. (b, e) φ and ψ are mutually exclusive. (c, f) φ and ψ are jointly exhaustive. Regions ruled out by sentences are shaded in the top row—in green for φ and in blue for ψ. The regions left open are hatched in the bottom row—hatched horizontally for φ and vertically for ψ.
When φ ⊨ ψ (see a and d above), the implied sentence ψ cannot rule out any possibility not already ruled out by the implying sentence φ, so the region ruled out by φ must include the region ruled out by ψ (and the region left open by φ must therefore be included in the region left open by ψ). If φ and ψ are mutually exclusive (see b and e above), there can be no overlap in the regions they leave open so the regions ruled out by the two must together cover the full range of possibilities. Here φ rules out all worlds at the left of the rectangle and ψ rules out all worlds at the right, with both ruling out a swath of worlds in the middle. It is the same thing to say that there is no overlap in the worlds they leave open, a situation depicted on the right (in e). Finally, when φ and ψ are jointly exhaustive, the situation is reversed (see c and f above): the regions left open by the two must together cover all possibilities so the regions they rule out cannot overlap. In the diagram a swath of worlds through the middle is left open by both.
When none of these relations hold between a pair of sentences φ and ψ—that is, when each of four patterns of truth values for the two appears in some possible world—we will say that φ and ψ are logically independent. Not only are logically independent sentences unordered by implication, they are not tied by any deductive relation. And this sort of thing holds for most pairs of sentences. Although sentences on different topics almost always provide examples, logically independent sentences do not need to differ in subject matter. For example, the sentences The package will arrive next week and The package will arrive on a Wednesday (a pair of sentences mentioned in 1.2.4) are logically independent since it is possible for the package to arrive next week but not on Wednesday (so the first doesn’t imply the second), for it to arrive on a Wednesday but not next week (so the first isn’t implied by the second), for it to arrive next Wednesday (so they aren’t mutually exclusive), and for it to arrive neither next week nor on a Wednesday (so they aren’t jointly exhaustive).