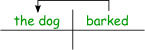7.1.1. Theories of quantifier phrases

In 6.1.6 individual terms like Spot and the dog were distinguished from other singular noun phrases like every dog, no dog, and a dog, whose semantic function is not to make definite references to single objects. We call phrases of the latter sort quantifier phrases and we will call words like every, no, and a that are used to form them quantifier words. The term quantifier here is intended to suggest the semantic function of these phrases: they serve to say how many objects of a certain kind have a certain property. Thus Every dog likes bones says that all objects of the kind indicated by the term dog have the property expressed by the predicate [ _ likes bones] while No dog climbs trees says that 0 objects of this kind have the property of climbing trees. Sentences with an indefinite article—for example, A dog has been digging in the garden—are particularly instructive. The claim made by this sentence is that at least one dog has the property of having been digging in the garden. (Or else that there was at least one dog that had the property of digging in the garden. The difference between the two interpretations is important but is one we cannot explore in this course. In the first we regard the tense of the sentence as part of the predicate while in the second we understand it to apply to the whole sentence. The second interpretation would preclude further analysis without some means of representing tense, something we will not explore.) Although the truth of this sentence can, in some cases, be traced to the activities of an individual dog it is not a claim about any individual dog but rather about the class of dogs as a whole. That is why its denial, No dog has been digging in the garden, does not give even the appearance of concerning an individual dog.

The study of quantifier phrases is one of the oldest parts of deductive logic but it is also the part that was last to be fully developed. The study of sentences like the examples above was the heart of Aristotle’s work in logic and it is the one part of logic that was preserved in periods (such as the Renaissance and early modern era) when interest in logic dwindled and much of truth-functional logic was ignored or forgotten. However, Aristotle’s account of these sentences was not fully satisfactory, and the problems they raised were not solved completely until the work of Frege.

Aristotle’s treatment of quantifier phrases is the basis of the traditional theory of syllogisms. That theory was principally concerned with the sentences that contained quantifier phrases and it applied directly only to sentences that could be restated with a single quantifier phrase in subject position. It could not account for the validity of arguments that depended on the presence and interaction of several quantifier phrases in the same sentence. As an example of the latter, a traditional one, notice that Every horse is a mammal implies Any head of a horse is a head of a mammal, an implication that turns on the function of the two quantifier phrases a horse and a mammal in the conclusion.

Medieval logicians began to develop an account of quantifier phrases that looked at individual phrases rather than at a limited variety of sentences containing them. The idea was to look at quantifier phrases, like individual terms, as serving to refer—with individual terms and the various quantifier phrases referring in different ways. The sort of reference, or supposition, would depend, in the case of quantifier phrases, on the quantifier word used and also on the place of the quantifier phrase in the sentence. Thus we might speak, as indeed we have, of Spot and the dog as making a definite reference. And, in a similar way, we might speak of every dog and no dog as both making a general reference to dogs (differing in whether they say they all have or all lack a given property) and of a dog as making an indefinite reference to a dog (since no more than one dog need be in question but no particular dog is crucial). This, by itself, does not settle the problem of multiple quantifier phrases but it does provide an approach to quantifier phrases that could be applied to each of several phrases in the same sentence.

The problem with a theory like this lies in the possibility that the kind of reference a quantifier phrase exhibits depends not only on the quantifier word it contains and its place in a sentence but also on its relation to other quantifier phrases. The ambiguity of sentences like the following one shows that the interaction of quantifier phrases can be important:

This could be understood to assert either the weak claim that each juror was interviewed or the stronger claim that there was a single reporter who interviewed them all. The difference between these two claims can be brought out by restating the sentence to make one or the other of the quantifier phrases the subject followed by the phrase is such that—that is, by using the device of expansion that we used for a different purpose in 6.2.

If we were to account for this ambiguity by something like a theory of supposition, we would have to find some sort of ambiguity in the quantifier phrases. The most natural way of doing this would be to say that a phrase like a reporter can have two sorts of reference, either a fixed indefinite reference or a variably indefinite reference (giving rise to the strong and weak readings, respectively); and this is roughly the account given by medieval logicians working on the theory of supposition.

The difficulty is that this sort of ambiguity is not the only one that can arise. For example, consider the following:

This is four ways ambiguous, with the interpretations indicated in the following table:

The strongest reading entails all the rest and all entail the weakest reading, but neither of the two intermediate readings entails the other.

The problem that this example poses for a theory of supposition is not simply that the different meanings of a question have begun to mount up implausibly but that the differences cannot be described without reference to other quantifier phrases. That is, a question could be said to exhibit a variably indefinite reference not only in the weakest reading but also in the two intermediate readings. These three readings differ because the variation in reference is allowed to depend on different factors: on both the reporter and the juror (the weakest), on the reporter only (the first intermediate reading), or on the juror only (the second intermediate reading). And this makes it seem that the differences lie not in the way a single quantifier phrase refers but in the way the sentence as a whole is put together.

One way of diagnosing the problem is to note that, while the theory of supposition provides the resources for a more subtle description of the ways sentences can be put together than is available in Aristotelian logic, it does not provide a way of describing the structure of sentences in varying levels of detail comparable to the gradually developing analyses that we can offer using connectives. There were hints of another approach in the Middle Ages but nothing was worked out fully until Frege’s Begriffschrift (or ‘Concept notation’) of 1879. And it is hard to see how anything like Frege’s solution to the problem of quantifier phrases could have been developed much earlier; for it depended on his understanding of predicates as expressing truth-valued functions of objects. This idea was a considerable extension of the concept of a function current in his day, and this had already been extended far beyond anything that might have occurred to a mathematician in the 18^th century, to say nothing of a philosopher in the Middle Ages.

Still the medieval hints and Frege’s final approach handled the problem we have been considering in a similar way. In both views, predicates come first and quantifier phrases are added to them—and added to them in a certain order. The different readings we may give to the resulting sentence then depend on the order in which the quantifier phrases were added. In the case of Every reporter asked a question of each juror, the strongest reading comes when a question is added last, for then we are saying that at least one question has the property expressed by [every reporter asked _ of every juror]. The weakest reading comes when we add this quantifier phrase first, for then we say only that the predicate [ _ asked a question of _ ]—roughly, [ _ questioned _ ]—is true of every reporter and juror. The other two possibilities come when a question has been added to the sentence before one but not the other of the phrases every reporter and each juror.

What distinguished Frege’s approach was that he went beyond the metaphor of quantifier phrases lining up to be added to a sentence. Instead, he spoke of quantifier phrases as signs for operations that apply to predicates just as predicates are operations that apply to individual terms. Thus, on this view, the grammatical similarity between individual terms and quantifier phrases disguises the semantic difference that is shown in Figure 7.1.1-1:

a predicate applies to an individual term to say something about the object it refers to		a quantifier phrase applies to a predicate to say something about the property it expresses
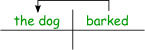
A		B

Fig. 7.1.1-1. The semantic roles of an individual term (A) and a quantifier phrase (B).

This kind of analysis can be applied to a sentence several times over by using the device of expansion. For example, the second intermediate reading of the quadruply ambiguous sentence above could be expressed along with its component predicates as follows:

Here each quantifier phrase is seen to apply to a predicate that may contain previously applied quantifier phrases.