6.4.x. Exercise questions
| 1. | Each of a, b, and c gives a structure in one of the two sorts of presentation described in this section—by a diagram or by tables. Present each of them in the other way. | |
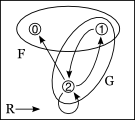
| a. |

|
|
| b. |
|
|
|
| c. |
|
|
|
|
| 2. | Calculate a truth value for each of the following sentences on the structure used as the chief example in this section (see, for example, Figure 6.4.2-7): | |
| a. | (Fa ∨ Gb) → Rab | |
| b. | R(fca)(fac) | |
| c. | fab = fba | |
| 3. | Use derivations to check each of the claims below; if a claim of entailment fails, use either tables or a diagram to present a structure that divides an open gap. | |
| a. | a = a → Fa ⇒ Fa | |
| b. | ¬ (Fa ∧ Fb) ⇒ ¬ Fa → ¬ Fb | |
| c. | a = b ∨ b = a ⇒ a = b ∧ b = a | |
| d. | Fa → a = b, ga = b, Ra(ga) → Fa, F(ga) ⇒ Raa → R(ga)(ga) | |
| e. | a = b → Rac, ¬ a = b → Rbc ⇒ Rbc | |
For more exercises, use the exercise machine.