phi_270_F05_test

Phi 270 F05 test 4

Analyze the sentences below in as much detail as possible, providing a key to the non-logical vocabulary you use. Restate 1 using an unrestricted quantifier.
1.	`Everyone knew the tune.` [Remember to restate your answer to this using an unrestricted quantifier.] answer
2.	`Sam heard only tunes that he knew.` [Remember to restate your answer in 2 using an unrestricted quantifier.] answer
3.	`No one liked everything on the menu.` answer

Synthesize an English sentence with the following logical form; that is, produce a sentence that would have the following analysis:
4.	(∀x: Px) ¬ Fsx P: [ _ `is a person`]; F: [ _ `fit` _ ]; s: `the shoe` answer

Use derivations to show that the following arguments are valid. You may use any rules.
5.	∀x (Fx ∧ Gx) ∀x (Gx ∧ Fx) answer
6.	∀x ∀y (Gy → Rxy) ∀x (Fx → Gx) ∀x (Fx → ∀y Ryx) answer

Use a derivation to show that the following argument is not valid and present a counterexample by describing a structure that divides an open gap. (You may describe the structure either by depicting it in a diagram, as answers in the text usually do, or by giving tables.)
7.	∀x (Fx → Rax) Fa ∀x Rxa answer

Phi 270 F05 test 4 answers

1.	`Everyone knew the tune` `Everyone is such that (he or she knew the tune)` (∀x: x `is a person`) x `knew` `the tune` (∀x: Px) Kxt ∀x (P → Kxt) K: [ _ `knew` _ ]; P: [ _ `is a person`]; t: `the tune`

Sam heard only tunes that he knew

only tunes that Sam knew are such that (Sam heard them)

(∀x: ¬ x is a tune that Sam knew) ¬ Sam heard x

(∀x: ¬ (x is a tune ∧ Sam knew x)) ¬ Hsx

(∀x: ¬ (Tx ∧ Ksx)) ¬ Hsx

[ _ heard _ ]; K: [ _ knew _ ]; T: [ _ is a tune]; s: Sam

A different but equally plausible interpretation would be to treat tunes as a bounds indicator; this interpretation would be analyzed as (∀x: Tx ∧ ¬ Ksx) ¬ Hsx. This is also the analysis of Sam heard no tunes he didn’t know.

No one liked everything on the menu

No one is such that (he or she liked everything on the menu)

(∀x: x is a person) ¬ x liked everything on the menu

(∀x: Px) ¬ everything on the menu is such that (x liked it)

(∀x: Px) ¬ (∀y: y is on the menu) x liked y

(∀x: Px) ¬ (∀y: Oym) Lxy

L: [ _ liked _ ]; O: [ _ is on _ ]; P: [ _ is a person]; m: the menu

(∀x: x is a person) ¬ the shoe fit x

No one is such that (the shoe fit him or her)

The shoe fit no one

(∀x: x is a person) ¬ the shoe fit x

(∀x: x is a person) the shoe didn’t fit x

Everyone is such that (the shoe didn’t fit him or her)

The shoe didn’t fit anyone

The sentence The shoe didn’t fit everyone is not the best synthesis since it is likely to be understood as the denial of The shoe fit everyone—i.e., as ¬ (∀x: Px) Fsx.

	│∀x (Fx ∧ Gx)	a:2
	├─
	│ⓐ
2 UI	││Fa ∧ Ga	3
3 Ext	││Fa	(6)
3 Ext	││Ga	(5)
	││
	│││●
	││├─
5 QED	│││Ga	4
	││
	│││●
	││├─
6 QED	│││Fa	4
	│├─
4 Cnj	││Ga ∧ Fa	1
	├─
1 UG	│∀x (Gx ∧ Fx)

	│∀x ∀y (Gy → Rxy)	b:6
	│∀x (Fx → Gx)	a:4
	├─
	│ⓐ
	│││Fa	(5)
	││├─
	│││ⓑ
4 UI	││││Fa → Ga	5
5 MPP	││││Ga	(8)
6 UI	││││∀y (Gy → Rby)	a: 7
7 UI	││││Ga → Rba	8
8 MPP	││││Rba	(9)
	││││●
	│││├─
9 QED	││││Rba	3
	││├─
3 UG	│││∀y Rya	2
	│├─
2 CP	││Fa → ∀y Rya	1
	├─
1 UG	│∀x (Fx → ∀y Ryx)

	│∀x (Fx → Rax)	a:1, b:4
	│Fa	(2)
	├─
1 UI	│Fa → Raa	2
2 MPP	│Raa
	│
	│ⓑ
4 UI	││Fb → Rab	6
	││
	│││¬ Rba
	││├─
	│││││¬ Fb
	││││├─
	│││││○	Fa,Raa,¬Rba,¬Fb⇏⊥
	││││├─
	│││││⊥	7
	│││├─
7 IP	││││Fb	6
	│││
	││││Rab
	│││├─
	││││○	Fa,Raa,¬Rba,Rab⇏⊥
	│││├─
	││││⊥	6
	││├─
6 RC	│││⊥	5
	│├─
5 IP	││Rba	3
	├─
3 UG	│∀x Rxa

Counterexample presented by a diagram

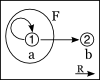
Counterexample presented by tables

range: 1, 2

a	b
1	2

τ	Fτ
1	T
2	F

R	1	2
1	T	T
2	F	F

This counterexample divides both gaps; but the specific value for F2 is needed only for the first gap and the specific value for R12 is needed only for the second.