phi_270_F05_test

Phi 270 F05 test 5

Analyze the following sentences in as much detail as possible, providing a key to the non-logical vocabulary (upper and lower case letters) appearing in your answer. Notice the special instructions given for each of 1, 2, and 3.
1.	`A bell rang.` [Give an analysis using a restricted quantifier, and restate it using an unrestricted quantifier.] answer
2.	`There was a storm but no flight was delayed.` [Avoid using ∀ in your analysis of any quantifier phrases in this sentence.] answer
3.	`Everyone was humming a tune.` [On one way of understanding this sentence, it would be false if people were humming different tunes. Analyze it according to that interpretation.] answer
4.	`Tom saw at least two snowflakes.` answer

Analyze the sentence below using each of the two ways of analyzing the definite description. That is, give an analysis that uses Russell’s treatment of definite descriptions as quantifier phrases as well as one that uses the description operator.
5.	`Ann saw the play.` answer

Use a derivation to show that the following argument is valid. You may use any rules.
6.	∃x (Fa → Gx) Fa → ∃x Gx answer

Use a derivation to show that the following argument is not valid, and use either a diagram or tables to present a counterexample that divides an open gap of your derivation.
7.	∃x Fx ∃x Rxa ∃x (Fx ∧ Rxa) answer

Complete the following to give a definition of inconsistency in terms of truth values and possible worlds:

8.	A set Γ of sentences is inconsistent (in symbols, Γ ⇒ or, equivalently, Γ ⇒ ⊥) if and only if … answer

Complete the following truth table for the two rows shown. In each row, indicate the value of each compound component of the sentence on the right by writing the value under the main connective of that component (so, in each row, every connective should have a value under it); also circle the value that is under the main connective of the whole sentence.

→

∧

∨

answer

Phi 270 F05 test 5 answers

1.	`A bell rang` `Some bell is such that (it rang)` (∃x: x `is a bell`) x `rang` (∃x: Bx) Rx ∃x (Bx ∧ Rx) B: [ _ `is a bell`]; R: [ _ `rang`]

There was a storm but no flight was delayed

There was a storm ∧ no flight was delayed

Something was a storm ∧ ¬ some flight was delayed

Something is such that (it was a storm) ∧ ¬ some flight is such that (it was delayed)

∃x x was a storm ∧ ¬ (∃x: x is a flight) x was delayed

∃x Sx ∧ ¬ (∃x: Fx) Dx

D: [ _ was delayed]; F: [ _ is a flight]; S: [ _ was a storm]

Everyone was humming a tune

Some tune is such that (everyone was humming it)

(∃x: x is a tune) everyone was humming x

(∃x: Tx) everyone is such that (he or she was humming x)

(∃x: Tx) (∀y: y is a person) (y was humming x)

(∃x: Tx) (∀y: Py) Hyx

H: [ _ was humming _ ]; P: [ _ is a person]; T: [ _ is a tune]

Everyone is such that (he or she was humming a tune) could be true even though people were humming different tunes, so an analysis of it would not be a correct answer.

4.	`Tom saw at least two snowflakes` `At least two snowflakes are such that (Tom saw them)` (∃x: x `is a snowflake`) (∃y: y `is a snowflake` ∧ ¬ y = x) (`Tom saw` x ∧ `Tom saw` y) (∃x: Fx) (∃y: Fy ∧ ¬ y = x) (Stx ∧ Sty) F: [ _ `is a snowflake`]; S: [ _ `saw` _ ]; t: `Tom`

5.	Using Russell’s analysis: `Ann saw the play` `The play is such that (Ann saw it)` (∃x: x `is a play` ∧ (∀y: ¬ y = x) ¬ y `is a play`) `Ann saw` x (∃x: Px ∧ (∀y: ¬ y = x) ¬ Py) Sax also correct: (∃x: Px ∧ ¬ (∃y: ¬ y = x) Py) Sax or: (∃x: Px ∧ (∀y: Py) x = y) Sax

Using the description operator:

Ann saw the play

S Ann the play

Sa (Ix x is a play)

Sa(Ix Px)

P: [ _ is a play]; S: [ _ saw _ ]; a: Ann

	│∃x (Fa → Gx)	2
	├─
	││Fa	(3)
	│├─
	││ⓑ
	│││Fa → Gb	3
	││├─
3 MPP	│││Gb	(4)
4 EG	│││∃x Gx	X,(5)
	│││●
	││├─
5 QED	│││∃x Gx	2
	│├─
2 PCh	││∃x Gx	1
	├─
1 CP	│Fa → ∃x Gx

The order of CP and PCh can be reversed in these and the use of MPP in the second could come after NcP and UI.

	│∃x (Fa → Gx)	2
	├─
	││Fa	(3)
	│├─
	││ⓑ
	│││Fa → Gb	3
	││├─
3 MPP	│││Gb	(6)
	│││
	││││∀x ¬ Gx	b:5
	│││├─
5 UI	││││¬ Gb	(6)
	││││●
	│││├─
6 Nc	││││⊥	4
	││├─
4 NcP	│││∃x Gx	2
	│├─
2 PCh	││∃x Gx	1
	├─
1 CP	│Fa → ∃x Gx

	│∃x Fx	1
	│∃x Rxa	2
	├─
	│ⓑ
	││Fb	(5)
	│├─
	││ⓒ
	│││Rca	(7)
	││├─
	││││∀x ¬ (Fx ∧ Rxa)	b:4, c:6, a:8
	│││├─
4 UI	││││¬ (Fb ∧ Rba)	5
5 MPT	││││¬ Rba
6 UI	││││¬ (Fc ∧ Rca)	7
7 MPT	││││¬ Fc
8 UI	││││¬ (Fa ∧ Raa)	9
	││││
	│││││││¬ Fa
	││││││├─
	│││││││○	Fb,Rca,¬Rba,¬Fc,¬Fa ⇏ ⊥
	││││││├─
	│││││││⊥	11
	│││││├─
11 IP	││││││Fa	10
	│││││
	│││││││¬ Raa
	││││││├─
	│││││││○	Fb,Rca,¬Rba,¬Fc,¬Raa ⇏ ⊥
	││││││├─
	│││││││⊥	12
	│││││├─
12 IP	││││││Raa	10
	││││├─
10 Cnj	│││││Fa ∧ Raa	9
	│││├─
9 CR	││││⊥	3
	││├─
3 NcP	│││∃x (Fx ∧ Rxa)	2
	│├─
2 PCh	││∃x (Fx ∧ Rxa)	1
	├─
1 PCh	│∃x (Fx ∧ Rxa)

range: 1, 2, 3

a	b	c
1	2	3

τ	Fτ
1	F
2	T
3	F

R	1	2	3
1	F	F	F
2	F	F	F
3	T	F	F

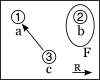
This interpretation divides both gaps; the value for F1 is needed only for the first gap and the value for R11 is needed only for the second.

8.	A set Γ of sentences is inconsistent if and only if there is no possible world in which all members of Γ are true or A set Γ of sentences is inconsistent if and only if, in each possible world, at least one member of Γ is false

→

∧

∨

Ⓣ

Ⓕ