phi_270_F03_test

Phi 270 F03 test 5

Analyze the following sentences in as much detail as possible, providing a key to the non-logical vocabulary (upper and lower case letters) appearing in your answer. Notice theadditional instructions given for the first.
1.	`Tom sent something to Sue` answer
2.	`Everyone heard a sound`. [This is ambiguous but you need only analyze one interpretation; justchoose the one that seems most natural to you.] answer
3.	`There is someone who knows just one other person.` answer

Analyze the sentence below using each of the two ways of analyzing the definite description the package. That is, analyze it using Russell’s analysis of definite descriptions as quantifier phrases and then analyze it again using the description operator.
4.	`The package rattled.` answer

Use derivations to show that the following argument is valid. You may use any rules.
5.	∃x Fx ∀x Gx ∃x (Fx ∧ Gx) answer

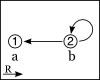
Use a derivation to show that the following argument is not valid and use either tables or a diagram to describe a structure dividing an open gap.
6.	∃x ∀y Rxy ∃x Rax answer

Complete the following to give a definition of equivalence in terms of truth values and possible worlds:

7.	A sentence φ is equivalent to a sentence ψ (i.e., φ ⇔ ψ) if and only if … answer

Answer the following question and explain your answer in terms of the definitions of the basic concepts it involves.
8.	Suppose you are told that (i) φ ⇒ ψ and (ii) ψ is inconsistent with χ (i.e., the set formed of the twois inconsistent). What can you conclude about the relation between of φ and χ? That is, what patterns of truth values for the two are ruled out (if any are); and, if any are ruled out, what logical relation or relations holds as a result. answer

Complete the following truth table by calculating the truth value of the sentence on each of the given assignments. In each row, write under each connective the value of the component of which it is the main connective and circle the truth value of the sentence as a whole.

∧

∨

→

answer

Phi 270 F03 test 5 answers

1.	`Tom sent something to Sue` ∃x `Tom sent` x `to Sue` ∃x Ntxs C: [ _ `sent` _ `to` _ ]; s: `Sue`; t: `Tom`

2.	`Everyone heard a sound` (∃x: x `is a sound`) `everyone heard` x (∃x: x `is a sound`) (∀y: y `is a person`) y `heard` x (∃x: Sx) (∀y: Py) Hyx H: [ _ `heard` _ ]; P: [ _ `is a person`]; S: [ _ `is a sound`]

There is someone who knows just one other person

∃x x is a person who knows just one other person

∃x (x is a person ∧ x knows just one other person)

∃x (Px ∧ (∃y: Py ∧ ¬ y = x) x knows y and no other person besides y)

∃x (Px ∧ (∃y: Py ∧ ¬ y = x) (Kxy ∧ x knows no other person besides y))

∃x (Px ∧ (∃y: Py ∧ ¬ y = x) (Kxy ∧ (∀z: Pz ∧ ¬ z = x ∧ ¬ z = y) ¬ Kxz))
or:
∃x (Px ∧ (∃y: Py ∧ ¬ y = x) (Kxy ∧ (∀z: Pz ∧ ¬ z = x ∧ Kxz) y = z))

K: [ _ knows _ ]; P: [ _ is a person]

using Russell’s analysis:

The package rattled

(∃x: x and only x is a package) x rattled

( ∃x: x is a package ∧ (∀y: ¬ y = x) ¬ y is a package) Rx

(∃x: Px ∧ (∀y: ¬ y = x) ¬ Py) Rx
or:
(∃x: Px ∧ (∀y: Py) x = y) Rx

using the description operator:

The package rattled

R(the package)

R (Ix x is a package)

R(Ix Px)

P: [ _ is a package]; r: [ _ rattled]

	│∃x Fx	1
	│∀x Gx	a: 2
	├─
	│ⓐ
	││Fa	(3)
	│├─
2 UI	││Ga	(3)
3 Adj	││Fa ∧ Ga	X, (4)
4 EG	││∃x (Fx ∧ Gx)	X, (5)
	││●
	│├─
5 QED	││∃x (Fx ∧ Gx)	1
	├─
1 PCh	│∃x (Fx ∧ Gx)

	│∃x ∀y Rxy	1
	├─
	│ⓑ
	││∀y Rby	a:3, b:4
	│├─
	│││∀x ¬ Rax	a:5, b:6
	││├─
3 UI	│││Rba
4 UI	│││Rbb
5 UI	│││¬ Raa
6 UI	│││¬ Rab
	│││○	Rba,Rbb,¬Raa,¬Rab ⇏ ⊥
	││├─
	│││⊥	2
	│├─
2 NcP	││∃x Rax	1
	├─
1 PCh	│∃x Rax

7.	φ and ψ are equivalent if and only if there is no possible world in which they have different truth values (or: if and only, in every possible world, each has the same value as the other)

φ and χ are inconsistent. That is, φ and χ cannot be both true because ψ will be true when φ is, and ψ and χ cannot be both true. Other patterns of values for φ and χ are possible because they are not ruled out for ψ and χ by the fact that they are inconsistent and, for all weknow, φ and ψ may be equivalent.

∧

∨

→

Ⓕ

Ⓣ