A restricted universal sentence (∀x: ρx) θx is a generalization written symbolically. Its domain is the extension of ρ and its attribute is the property expressed by θ. Since we have already discussed the problem of identifying the domains and attributes of English sentences, we can complete our discussion of analyzing generalizations by saying how to choose restricting and quantified predicates ρ and θ so that the domain and attribute of the generalization (∀x: ρx) θx are what we want them to be. There is little to be said in the case of attributes. The quantified predicate θ of (∀x: ρx) θx should express the attribute, so it should be a symbolic version of the English quantified predicate in cases where the generalization is affirmative and a symbolic version of the denial of that predicate is cases where the generalization is negative. Notice that the quantified predicate appearing in the analysis of a negative generalization will correspond to the negation of the quantified predicate of the original English sentence; since symbolic generalizations are always affirmative, negative generalization is expressed by explicit negation in the quantified formula.
There is only a little more to be said in the case of domains. To get from a domain to a restricting predicate, we need a predicate that is true of just the things in the domain. When C is a term picking out the domain, a predicate of the form λx (x is a C) will be true of the objects in this class. When the domain is the complement of the class picked out by C, a predicate of the form λx (x is not a C)—i.e., λx (¬ x is a C)—may be used.
There is one complication to this in a case that is special but occurs quite frequently. The quantifier phrases Everyone and No one have the word one as their class indicator. But λx (x is a one) is ungrammatical and anyway does little to delimit a domain. So we are forced to treat everyone and no one as we would the synonymous (or nearly synonymous) every person and no person and use λx (x is a person) as the domain predicate.
Let us apply these ideas to some earlier examples of generalizations, beginning with Every dog barks. This is affirmative and direct. So the quantified predicate of the English sentence, λx (x barks), expresses the attribute of the generalization and can also give us the attribute predicate of the symbolic form. The domain is the class of dogs, so the domain predicate can be λx (x is a dog). Putting the two together we get the following symbolic renderings of the quantifier phrase, using the restricted and unrestricted quantifiers, respectively:
(∀x: x is a dog) x barks
∀x (x is a dog → x barks)
These may be read as Everything, x, such that x is a dog is such that x barks and Everything, x, is such that if x is a dog then x barks.
The example No dog climbs trees was also direct but was negative. Thus we may use the same domain predicate but the quantified predicate of the symbolic form should be the denial of the English quantified predicate. This gives us the forms
(∀x: x is a dog) ¬ x climbs trees
∀x (x is a dog → ¬ x climbs trees),
which may be read as Everything, x, such that x is a dog is such that not x climbs trees and Everything, x, is such that if x is a dog then not x climbs trees.
Our first example of a negative and complementary generalization was Only trucks were advertised. The attribute here is the property of not having been advertised so the quantified predicate of the symbolic form may be λx (¬ x was advertised). The domain is the class of non-trucks. The restricting predicate can then be λx (¬ x is a truck) and the symbolic forms are these:
(∀x: ¬ x is a truck ) ¬ x was advertised
∀x (¬ x is a truck → ¬ x was advertised)
These may be read as Everything, x, such that not x is a truck is such that not x was advertised and Everything, x, is such that if not x is a truck then not x was advertised.
More generally, we can offer the following symbolic versions of the three basic patterns of generalization we identified:
| Direct and affirmative: |
Every C is such that ...it...
(∀x: x is a C) ...x...
|
| Direct and negative: |
No C is such that ...it...
(∀x: x is a C) ¬ ...x...
|
| Complementary and negative: |
Only Cs are such that ...they...
(∀x: ¬ x is a C) ¬ ...x...
|
If the domain C of a direct generalization is the whole referential range, the restricting predicate λx (x is a C) is not at all restrictive and we may use instead a simpler form with an unrestricted universal quantifier applying to the attribute predicate. So we have the following special cases of the direct forms of generalization:
| Unrestricted and affirmative: |
Everything is such that ...it...
∀x ...x... |
| Unrestricted and negative: |
Nothing is such that ...it...
∀x ¬ ...x... |
A similar simplification would apply to complementary forms only if the class indicator was sure to pick out the empty set; you are invited to find an example.
These symbolic representations show us something about the relation between the English forms All Cs are such that ...they... and Only Cs are such that ...they.... If we represent these symbolically by applying unrestricted quantifiers to conditionals, we have the following (which are given with possible English readings below):
| All Cs are such that ...they... |
∀x ( x is a C → ...x...)
Everything, x, is such that (...x... if x is a C) |
| Only Cs are such that ...they... |
∀x ( ¬ x is a C → ¬ ...x...)
Everything, x, is such that (...x... only if x is a C) |
This gives us a reason for saying that all is to only as if is to only if. And we can compare the fact that an all-generalization implicates an only-generalization to the fact that an if-conditional implicates an only if-conditional. Just as biconditionals expressing conjunctions of if-conditionals and only-if-conditionals can be stated using the compound conjunction if and only if, conjunctions of the corresponding sorts of generalizations can be expressed using the compound quantifier term all and only. The effect of the latter phrase is to claim that the indicated class is identical with the extension of the quantified predicate, and this claim can be expressed symbolically either as a conjunction of generalizations or by an unrestricted universal applying to a biconditional predicate. For example, All and only winners of the first round are entitled to advance might be analyzed by either of the following:
(∀x: Wxf) Ex ∧ (∀x: ¬ Wxf) ¬ Ex
∀x ((Wxf → Ex) ∧ (¬ Wxf → ¬ Ex))
[E: λx (x is entitled to advance); W; λxy (x is a winner of y); f: the first round]
The second can be read as Everything, x, is such that (x is entitled to advance if and only if x is a winner of the first round).
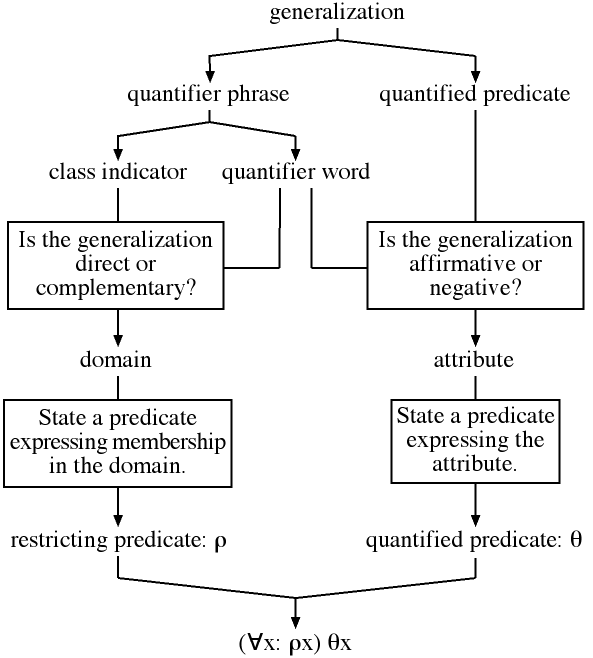
Figure 7.2.4-1 below provides an overview of the process of analyzing generalizations.

Fig. 7.2.4-1. The process of analyzing a generalization.
There are essentially four stages to the process:
| (i) | analyze the generalization into a quantifier phrase and quantified predicate (by restating it with the quantifier phrase as subject followed by is such that) and analyze the quantifier phrase into a quantifier word and class indicator; | |
| (ii) | find the domain and attribute of the generalization given the class indicator and quantified predicate, using the quantifier word to determine whether the generalization is direct or complementary and affirmative or negative; | |
| (iii) | state restricting and quantified predicates, which express membership in the domain and possession of the attribute, respectively; | |
| (iv) | combine the restricting and quantified predicates to state the generalization in symbolic form. |
The restricting and quantified formulas, ρx and θx should be stated as English sentences containing the variable x so that they themselves can then be subjected to analysis.