Phi 270 F98 Quiz 6

Phi 270 F98 quiz 6 (of 6) in pdf format

Analyze the following sentences in as much detail as possible, providing a key to the non-logical vocabulary (upper and lower case letters) appearing in your answer.
1.	`George traveled to LA by way of some town in Wyoming`. [Give this analysis also using an unrestricted quantifier.] [answer]
2.	`Everyone is afraid of something`. [This sentence is ambiguous. Analyze it in two different ways, and describe a situation in which the sentence is true on one of your interpretations and false on the other.] [answer]
3.	`Spot knew exactly one trick`. [answer]

4.	Analyze the sentence below using each of the two ways of analyzing definite descriptions. That is, analyze it using Russell's analysis of definite descriptions as quantifier phrases and then analyze it again using the description operator. `Tom opened the letter from Bulgaria` [answer]

Use derivations to show that the following argument is valid. You may use any rules.

(∃x: Fx) ∃y ¬ x = y

∃x (∃y: ¬ y = x) Fy

That is: Some finding is different from something ⇒ Something is such that something different from it is a finding [but don't hesitate to ignore the English if it doesn't help].
[answer]

Use a derivation to show that the following argument is not valid and describe a structure dividing an open gap.

∃x ∃y Rxy

∃x Rxx

[answer]

7.	Complete the following to give a definition of equivalence in terms of truth values and possible worlds: A sentence φ is equivalent to a sentence ψ if and only if ... [answer]

Describe a structure (i.e., an assignment of extensions to the non-logical vocabulary) which makes the 8 sentences at the left below all true.

fab = fba, ga = fab, fba = c, Fb, F(ga), Rab, ¬ Rba, R(ga)c
[answer]

[This question was on a topic not covered in F05] Use replacement by equivalence to put the following sentence into disjunctive normal form. Show how you reach your result; you may combine uses of associativity and commutativity with other principles in a single step but there should be no more than one use of De Morgan's laws or distributivity in each step.

¬ ((A ∧ B) ∨ (C ∨ D))

[answer]

Phi 270 F98 quiz 6 answers

George traveled to LA by way of some town in Wyoming
some town in Wyoming is such that (George traveled to LA by way of it)
(∃x: x is a town in Wyoming) George traveled to LA by way of x
(∃x: x is a town ∧ x is in Wyoming) George traveled to LA by way of x

(∃x: Tx ∧ Nxm) Rglx
∃x ((Tx ∧ Nxm) ∧ Rglx)

[N: λxy (x is in y); R: λxyz (x traveled to y by way of z); T: λx (x is a town); g: George; l: LA; m: Wyoming]

2.	first analysis: `Everyone is afraid of something` `everyone is such that (he or she is afraid of something)` (∀x: x `is a person`) x `is afraid of something` (∀x: Px) `something is such that (`x `is afraid of it)` (∀x: Px) ∃y x `is afraid of` y (∀x: Px) ∃y Axy
	second analysis: `Everyone is afraid of something` `something is such that (everyone is afraid of it)` ∃x `everyone is afraid of` x ∃x `everyone is such that (he or she is afraid of` x`)` ∃x (∀y: y `is a person`) y `is afraid of` x ∃x (∀y: Py) Ayx
	[A: λxy (x `is afraid of` y); P: λx (x `is a person`)] The first is true and the second false if all people are fearful but not all fearful of the same thing

Spot knew exactly one trick
Spot knew a trick ∧ ¬ Spot knew at least two tricks
(∃ x: x is a trick) Spot knew x ∧ ¬ (∃ x: x is a trick) (∃ y: y is a trick ∧ ¬ y = x) (Spot knew x ∧ Spot knew y)

(∃ x: Tx) Ksx ∧ ¬ (∃ x: Tx) (∃ y: Ty ∧ ¬ y = x) (Ksx ∧ Ksy)
or:
(∃ x: Tx) (Ksx ∧ (∀ y: Ty ∧ ¬ y = x) ¬ Ksy)
or:
(∃ x: Tx) (Ksx ∧ (∀ y: Ty ∧ Ksy) x = y)

[K: λxy (x knew y); T: λx (x is a trick); s: Spot]

4.	using Russell's analysis: `Tom opened the letter from Bulgaria` `the letter from Bulgaria is such that (Tom opened it)` (∃x: x `and only` x `is a` `letter from Bulgaria`) `Tom opened` x (∃x: x `is a letter from Bulgaria` ∧ (∀y: ¬ y = x) ¬ y `is a letter from Bulgaria`) Otx (∃x: x `is a letter` ∧ x `is from Bulgaria` ∧ (∀y: ¬ y = x) ¬ y `is a letter` ∧ y `is from Bulgaria`) Otx (∃x: (Lx ∧ Fxb) ∧ (∀y: ¬ y = x) ¬ (Ly ∧ Fyb)) Otx or: (∃x: (Lx ∧ Fxb) ∧ (∀y: Ly ∧ Fyb) x = y) Otx
	using the description operator: `Tom` `opened` `the letter from Bulgaria` Ot(`the letter from Bulgaria`) Ot(Ix x `is a letter from Bulgaria`) Ot(Ix (x `is a letter` ∧ x `is from Bulgaria`)) Ot(Ix (Lx ∧ Fxb))
	[F: λxy (x `is from` y); L: λx (x `is a letter`); O: λxy (x `opened` y); b: `Bulgaria`; t: `Tom`]

	│(∃x: Fx) ∃y ¬ x = y	1
	├─
	│ⓐ
	││Fa	(3)
	││∃y ¬ a = y	2
	│├─
	││ⓑ
	│││¬ a = b	(3)
	││├─
3 REG	│││(∃y: ¬ y = b) Fy	X, (4)
4 EG	│││∃x (∃y: ¬ y = x) Fy	X, (5)
	│││●
	││├─
5 QED	│││∃x (∃y: ¬ y = x) Fy	2
	│├─
2 PCh	││∃x (∃y: ¬ y = x) Fy	1
	├─
1 PRCh	│∃x (∃y: ¬ y = x) Fy

	│∃x ∃y Rxy	1
	├─
	│ⓐ
	││∃y Ray	2
	│├─
	││ⓑ
	│││Rab
	││├─
	││││∀x ¬ Rxx	a:4,b:5
	│││├─
4 UI	││││¬ Raa
5 UI	││││¬ Rbb
	││││○	Rab, ¬Raa, ¬Rbb ⇏ ⊥
	│││├─
	││││⊥	3
	││├─
3 NcP	│││∃x Rxx	2
	│├─
2 PCh	││∃x Rxx	1
	├─
1 PCh	│∃x Rxx

7.	A sentence φ is equivalent to a sentence ψ if and only if there is no possible world in which φ and ψ have different truth values

fab = fba, ga = fab, fba = c, Fb, F(ga), Rab, ¬ Rba, R(ga)c

alias sets	IDs	values
a	1	a: 1
b	2	b: 2
c fab fba ga	3	c: 3 f12: 3 f21: 3 g1: 3

resources	values
Fb F(ga) Rab ¬ Rba R(ga)c	F2: T F3: T R12: T R21: F R33: T

range: 1, 2, 3

a	b	c
1	2	3

f	1	2	3
1	1	3	1
2	3	1	1
3	1	1	1

τ	gτ
1	3
2	1
3	1

τ	Fτ
1	F
2	T
3	T

R	1	2	3
1	F	T	F
2	F	F	F
3	F	F	T

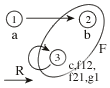
Only non-arbitrary values of f and g are shown

9.	[This question was on a topic not covered in F05] ¬ ((A ∧ B) ∨ (C ∨ ¬ D)) ⇔ ¬ (A ∧ B) ∧ ¬ (C ∨ ¬ D) ⇔ (¬ A ∨ ¬ B) ∧ (¬ C ∧ D) ⇔ (¬ A ∧ ¬ C ∧ D) ∨ (¬ B∧ ¬ C ∧ D)