φ  ψ 
| 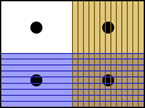 |
Fig. 1.2.3-1. The possibilities (shaded and hatched) ruled out by two propositions.
Logic is concerned with propositions in the way mathematics is concerned with numbers, but propositions are not numbers and perhaps the most notable difference between them is that, while numbers can be ordered in a linear way, the collection of propositions has a more complex structure. Although our examples in 1.2.2 formed a single chain from ⊤ to ⊥, it should be clear that we could have gone in many different directions to add content to any of the propositions that was not already absurd.
This metaphor of many directions suggests a space of more than one dimension. Although the structure of a collection of propositions not only from the 1-dimensional number line but also from the structure of ordinary 2- or 3-dimensional space, spatial metaphors and diagrams can help to elucidate its structure. These metaphors and can be associated with the term logical space introduced by the philosopher Ludwig Wittgenstein (1889-1951). We will actually use two different sorts of spatial metaphor. In one metaphor, possible worlds are the points of logical space and propositions determine regions in the space by drawing a boundary between the possibilities they rule out and the ones they leave open. In the other metaphor, possible worlds are the dimensions of the space and propositions are its points. In cases where there are finitely many possible worlds and propositions, the points of such a space can be thought of as the vertices of a figure that might be depicted in ordinary 2- or 3-dimensional space.
To see an example of the first sort of logical space, suppose there were only 4 possible worlds. A proposition will either rule out or leave open each of these possibilities. Figure 1.2.3-1 illustrates two such propositions; each rules out two of the four possibilities (in the shaded and hatched areas) and leaves open two others: the sentence φ rules out the two possibilities at the bottom of the diagram and ψ rules out the ones at the right. As a result both rule out the possible world in the lower right of the diagram and neither rules out the one in the upper left.
φ  ψ 
|  |
Fig. 1.2.3-1. The possibilities (shaded and hatched) ruled out by two propositions.
Of course, these are not the only propositions that can be expressed given this range of possibilities. A proposition has two options for each possible world: it may rule it out or leave it open. With 4 possible worlds this means that there are 2 × 2 × 2 × 2 = 16 propositions in all. Of these, six rule out two of the four possible worlds.
We can illustrate all 16 of these propositions by using a logical space of the second sort. Figure 1.2.3-2 depicts (in two dimensions) a 3-dimensional figure that is one possible representation of a 4-dimensional cube. It is labeled to suggest what sorts of sentences might express these propositions. You can imagine that the propositions φ (which appears at the left) and ψ (near the center) are the two propositions depicted in Figure 1.2.3-1.
The levels in the structure correspond to grades of strength, with Absurdity at the bottom ruling out all possible worlds and Tautology at the top ruling out none. A line connects propositions that differ only with respect to one possible world; the proposition lower in the diagram rules out this world and the one above it leaves the world open. Each of the four propositions immediately above Absurdity then leaves open just one possible world. Lines connecting worlds that differ with respect to a given proposition are parallel (in the 3-dimensional figure, not in its 2-dimensional projection). This is the sense in which possible worlds are the dimensions of this logical space.
The relation between the two sorts of diagram can be seen by replacing each proposition in Figure 1.2.3-2 by its representation using a diagram of the sort illustrated in Figure 1.2.3-1. Putting the two sorts of illustration together in this way gives us the following picture of the same 16 propositions.
The spacing of the nodes differs between Figures 1.2.3-2 and 1.2.3-3 but the left-to-right order at each level is the same and the regions associated with φ and ψ are the same as those depicted in Figure 1.2.3-1.
The whole structure of Figure 1.2.3-2 can be seen as a complex diamond formed of four diamonds whose corresponding vertices are linked. A simple diamond is the structure of the 2 × 2 = 4 propositions we would have with only 2 possible worlds. The structure in Figure 1.2.3-2 doubles the number of possible worlds and squares the number of propositions. If we were to double the number of possible worlds again to 8, we would square the number of propositions to get 256. The structure they would form could be obtained by replacing each node in the structure of Figure 1.2.3-2 by a small structure of the same form and replacing each line by a bundle of 16 lines connecting the corresponding nodes. To get a sense of the structure of the set of propositions for a realistically large set of possible worlds, imagine carrying out this process over and over again.
The result will always have an upper and lower limit (⊤ and ⊥) and many different nodes on each of its intermediate levels. As the number of possible worlds increases the distribution of possible worlds among the various degrees of strength (which is 1, 4, 6, 4, 1 in Figure 1.2.3-2) will more and more closely approximate a bell curve. But the bell shape of the curve will also narrow significantly. When there are only 10 possible worlds, the two propositions at the extremes still make up 0.2% of all propositions. But once there are 100 possible worlds, 99.9% of the propositions are found in the middle of third of the degrees of strength and with 1000 possible worlds 99.9% are found in the middle 1/10 (i.e., among those that rule out between 450 and 550 possible worlds). Eventually, a graph of the distribution would appear as a single spike in middle. And the height of this spike would be so great relative to number of different grades of strength that, were the scales of the two axes the same, the whole graph would be this single line. In short, the space of propositions is so far from a being a line from ⊤ to ⊥ that the distance from ⊤ to ⊥ vanishes in comparison to the spread of the space near its mid-point.
Of course, with any substantial number of possible worlds, we are dealing with vast numbers of propositions (for example, already about 10301 when there are only 1000 possible worlds), and tiny percentages of vast numbers can still be enormous. So there is no shortage of propositions whose strength lies towards the extremes. For example, again with 1000 possible worlds, there are better than 8 trillion propositions that leave open 5 or fewer of these 1000 possibilities.
If we suppose that there are infinitely many possible worlds, these counts and percentages cease to make sense. But it is possible to distinguish different infinite quantities and the propositions that leave open or rule out a finite number of possibilities will be less numerous in this sense than those both leave open and rule out an infinite number. For example, if we suppose that there are as many possible worlds as there are integers (of which there are ℵ0, aleph-null—the first of a series of infinite quantities labeled with the alef symbol ℵ), we might arrange the grades of strength as follows:
| number of worlds | number of propositions | |
| ruled out | left open | |
| 0 | ℵ0 | 1 |
| 1 | ℵ0 | ℵ0 |
| 2 | ℵ0 | ℵ0 |
| ⋮ | ⋮ | |
| ℵ0 | ℵ0 | 2ℵ0 |
| ⋮ | ⋮ | |
| ℵ0 | 2 | ℵ0 |
| ℵ0 | 1 | ℵ0 |
| ℵ0 | 0 | 1 |
Each grade other than the extremes and the central one contains ℵ0 propositions. If we group all grades other than the central one together, we still have ℵ0 (one of the oddities about the arithmetic of infinite quantities). The population of the central grade is the larger infinite quantity 2ℵ0, which is the size of the set of all real numbers and is also the size of the set of all propositions formed from a collection of ℵ0 possible worlds. So in this space, the single central grade of strength has as many propositions as the whole space, and both the size of the next largest grades and the total number of grades is a smaller infinite quantity that vanishes in comparison.