Phi 270 F99 test 4

Phi 270 F99 test 4 in pdf format

Analyze the following sentences in as much detail as possible, providing a key to the non-logical vocabulary (upper and lower case letters) appearing in your answer.
1.	`Sam invited every vertebrate to the party, but only people accepted his invitation` [answer]
2.	`Tom didn't send anything to the printer` [answer]
3.	`No game that every child liked was complete` [answer]
Synthesize an English sentence whose analysis would yield the following form.
4.	(∀x: Px) (∀y: Ry ∧ Txy) Sy [P: λx (x `is a person`); R: λx (x `is a room`); S: λx (x `was reserved`); T: λxy (x `thought of` y)] [answer]

Use derivations to establish the validity of the following arguments. You may use attachment rules.

∀x (Fx → Gx)

∀x Fx → ∀x Gx

[answer]

∀x (∀y: Fyx) ¬ Py

(∀x: Px) ∀y ¬ Fxy

[answer]

Use a derivation to show that the following argument is not valid and describe a structure (by using either a diagram or tables) that divides one of the derivation's open gaps.

∀x (∀y: Fy) ¬ Rxy

∀x Rxx

∀x ∀y ¬ Rxy

[answer]

Phi 270 F99 test 3 answers

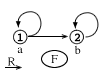
Sam invited every vertebrate to the party, but only people accepted his invitation

Sam invited every vertebrate to the party ∧ only people accepted Sam's invitation

every vertebrate is such that (Sam invited it to the party) ∧ only people are such that (they accepted Sam's invitation)

(∀x: x is a vertebrate) Sam invited x to the party ∧ (∀x:¬ x is a person) ¬ x accepted Sam's invitation

(∀x: Vx) Isxp ∧ (∀x:¬ Px) ¬ Ax(Sam's invitation)

(∀x: Vx) Isxp ∧ (∀x: ¬ Px) ¬ Ax(is)

[A: λxy (x accepted y); I: λxyz (x invited y to z); P: λx (x is a person); V: λx (x is a vertebrate); i: λx (x 's invitation); p: the party; s: Sam]

2.	`Tom didn't send anything to the printer` `everything is such that (Tom didn't send it to the printer)` ∀x `Tom didn't send` x `to the printer` ∀x ¬ `Tom` `sent` x `to` `the printer` ∀x ¬ Stxp [S: λxyz (x `sent` y `to` z); p: `the printer`; t: `Tom`]

No game that every child liked was complete

No game that every child liked is such that (it was complete)

(∀x: x was a game that every child liked) ¬ x was complete

(∀x: x was a game ∧ every child liked x) ¬ Cx

(∀x: x was a game ∧ every child is such that (he or she liked x)) ¬ Cx

(∀x: Gx ∧ (∀y: y was a child) y liked x) ¬ Cx

(∀x: Gx ∧ (∀y: Dy) Lyx) ¬ Cx

[C: λx (x was complete); D: λx (x was a child); G: λx (x was a game); L: λxy (x liked y)]

(∀x: x is a person) (∀y: y is a room ∧ x thought of y) y was reserved

(∀x: x is a person) (∀y: y is a room x thought of) y was reserved

(∀x: x is a person) every room x thought of was such that (it was reserved)

(∀x: x is a person) every room x thought of was reserved

everyone is such that (every room he or she thought of was reserved)

every room anyone thought of was reserved

	│∀x (Fx → Gx)	a:3
	├─
	││∀x Fx	a:4
	│├─
	││ⓐ
3 UI	│││Fa → Ga	5
4 UI	│││Fa	(5)
5 MPP	│││Ga	(6)
	│││●
	││├─
6 QED	│││Ga	2
	│├─
2 UG	││∀x Gx	1
	├─
1 CP	│∀x Fx → ∀x Gx

	│∀x (∀y: Fyx) ¬ Py	b:4
	├─
	│ⓐ
	││Pa	(6)
	│├─
	││ⓑ
	││││Fab	(5)
	│││├─
4 UI	││││(∀y: Fyb) ¬ Py	a:5
5 SB	││││¬ Pa	(6)
	││││●
	│││├─
6 Nc	││││⊥	3
	││├─
3 RAA	│││¬ Fab	2
	│├─
2 UG	││∀y ¬ Fay	1
	├─
1 RUG	│(∀x: Px) ∀y ¬ Fxy

	│∀x (∀y: Fy) ¬ Rxy	a:4,b:5
	│∀x Rxx	a:6,b:7
	├─
	│ⓐ
	││ⓑ
	││││Rab	(9)
	│││├─
4 UI	││││(∀y: Fy) ¬ Ray	a:8,b:9
5 UI	││││(∀y: Fy) ¬ Rby	b:10,a:11
6 UI	││││Raa	(8)
7 UI	││││Rbb	(10)
8 SC	││││¬ Fa
9 SC	││││¬ Fb
10 SC	││││¬ Fb
	││││
	││││││¬ Fa
	│││││├─
	││││││○	¬Fa,¬Fb,Rab,Raa,Rbb ⇏ ⊥
	│││││├─
	││││││⊥
	││││├─
	│││││Fa	11
	││││
	│││││¬ Rba
	││││├─
	│││││○	¬Fa,¬Fb,Rab,Raa,Rbb,¬Rba ⇏ ⊥
	││││├─
	│││││⊥	11
	│││├─
11 MCR	││││⊥	3
	││├─
3 RAA	│││¬ Rab	2
	│├─
2 UI	││∀y ¬ Ray	1
	├─
1 UI	│∀x ∀y ¬ Rxy

The structure below divides both gaps