Phi 270 F98 Quiz 3-4

Phi 270 F98 quiz 3 and part of quiz 4 (of 6) in pdf format
(questions from these two tests addressed the part of the course your test is designed to cover)

Analyze the sentences below in as much detail as possible without going below the level of sentences (i.e., without recognizing individual terms and predicates). Be sure that the unanalyzed components of your answer are complete and independent sentences and that you respect any grouping in the English. You may use right-to-left arrows to reflect English word order but you should then also restate your symbolic analysis with arrows running left to right and, in any case, you should restate it using English notation.
	3-1.	`If our message got there, they should be on their way` [answer]
	3-2.	`Unless we make reservations, we'll get a table only if it is a slow night` [answer]

3-3.

Check the following for validity using derivations; you may use attachment rules and detachment rules. If the derivation fails, present a counterexample that divides the premises from the conclusion.

A → (B → (C ∨ D))

¬ C → (A → ¬ B)

[answer]

3-4.	[This question was on a topic not covered in F04] Use replacement by equivalence to put the following sentence into disjunctive normal form. Show how you reach your result; you may combine uses of associativity and commutativity with other principles in a single step but there should be no more than one use of De Morgan's laws or distributivity in each step.
	¬ ((A ∨ ¬ B) ∧ (C ∧ A)) [answer]

3-5.

Analyze the sentence below in as much detail as possible, continuing the analysis when there are no more connectives by identifying predicates, functors, and individual terms. Be sure that the unanalyzed expressions in your answer are independent and that you respect any grouping in the English. (You need not state the result in English notation.)

If Sam is the winner of the trip, then the winner of the grand prize presented it to him

[answer]

3-6.	[This question was on a topic not covered in F04] Give two different expansions (using λ-notation for predicate abstracts) of the sentence below as a one-place predicate applied to a term: Pb ∧ Rab.
	Pb ∧ Rab [answer]

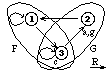
4-1.	Draw a diagram which presents the same interpretation as the following tables: referential range: {1,2,3} a c g t \| Ft Gt R \| 1 2 3 --------- ---\|-------- ---\|------- 2 3 2 1 \| T F 1 \| T F T 2 \| F T 2 \| T F F 3 \| T T 3 \| F T T [answer]

4-2.	Describe a structure (i.e., an assignment of extensions to the non-logical vocabulary) which makes the following sentences all true. (You may present the structure either using tables or, were possible, using diagrams.) fa = b, b = c, Pb, ¬ Pa, Ra(fa), R(fb)(fc), ¬ Rbc [answer]

Check each of the arguments below for validity using derivations. You need not present counterexamples to gaps that reach dead ends.

4-3.

fa = c

Rbc

a = b → Ra(fa)

[answer]

4-4.

Rab ∨ Rcb

a = b ∧ gb = gc

Rbc → Rcb

[answer]

Phi 270 F98 Answers to quiz 3 and part of quiz 4

3-1.	`If our message got there, they should be on their way` `our message got there` → `they should be on their way` M → W `if` M `then` W [M: `our message got there`; W: `they should be on their way`]

3-2.

¬ we will make reservations → we'll get a table only if it is a slow night
¬ we will make reservations → (¬ we'll get a table ← ¬ it will be a slow night)

¬ R → (¬ T ← ¬ S) or: ¬ R → (¬ S → ¬ T)
if not R then if not S then not T

[R: we will make reservations; S: it will be a slow night; T: we'll get a table]

3-3.

	│A → (B → (C ∨ D))	4
	├─
	││¬ C	(6)
	│├─
	│││A	(4)
	││├─
	││││B	(5)
	│││├─
4 MPP	││││B → (C ∨ D)	5
5 MPP	││││C ∨ D	6
6 MTP	││││D
	││││○	A, B, ¬ C, D ⇏ ⊥
	│││├─
	││││⊥
	││├─
3 RAA	│││¬ B	2
	│├─
2 CP	││A → ¬ B	1
	├─
1 CP	│¬ C → (A → ¬ B)

→

D))

→

Ⓣ

Ⓕ

3-4.

[This question was on a topic not covered in F04]

¬ ((A ∨ ¬ B) ∧ (C ∧ A))
⇔
¬ (A ∨ ¬ B) ∨ ¬ (C ∧ A)
⇔
(¬ A ∧ B) ∨ ¬ (C ∧ A)
⇔
(¬ A ∧ B) ∨ ¬ C ∨ ¬ A

[However, that problem was a typo;
I had really intended something along these lines:]

¬ ((A ∨ ¬ B) ∨ (C ∧ ¬ A))
⇔
¬ (A ∨ ¬ B) ∧ ¬ (C ∧ ¬ A)
⇔
(¬ A ∧ B) ∧ ¬ (C ∧ ¬ A)
⇔
(¬ A ∧ B) ∧ (¬ C ∨ A)
⇔
(¬ A ∧ B ∧ ¬ C) ∨ (¬ A ∧ B ∧ A)

[which could, but need not, be continued as follows:

⇔
(¬ A ∧ B ∧ ¬ C) ∨ (¬ A ∧ A)
⇔
¬ A ∧ B ∧ ¬ C ]

3-5.

If Sam is the winner of the trip, then the winner of the grand prize presented it to him
Sam is the winner of the trip → the winner of the grand prize presented the trip to Sam
s = the winner of the trip → [λxyz (x presented y to z)]the winner of the grand prize the trip Sam
s = [λx (the winner of x)] the trip → P(the winner of the grand prize)ts
s = nt → P([λx (the winner of x)] the grand prize)ts

s = nt → P(ng)ts

[P: λxyz (x presented y to z); g: the grand prize; n: λx (the winner of x); s: Sam; t: the trip]

3-6.	[This question was on a topic not covered in F04] The following are the possibilities; in the last, τ may be any term: [λx (Pb ∧ Rxb)]a, [λx (Px ∧ Rab)]b, [λx (Pb ∧ Rax)]b, [λx (Px ∧ Rax)]b, [λx (Pb ∧ Rab)]τ

4-1.

4-2.

alias sets
1: a
2: fa,b,c
3: fb,fc

range:1,2,3

 a b c
-------
 1 2 2

 t | ft
---|---
 1 | 2
 2 | 3
 3 | 1

 t | Pt
---|---
 1 | F
 2 | T
 3 | F

 R | 1 2 3
---|-------
 1 | F T F
 2 | F F F
 3 | F F T

 fa = b  b = c  Pb  ¬ Pa  Ra(fa)  R(fb)(fc)  ¬ Rbc
---------------------------------------------------
 21 T 2  2 T 2  T2  T F1  T1 21   T 32  32   T F22

4-3.

	│fa = c	a, b, fa=c, fb
	│Rbc	(2)
	├─
	││a = b	a=b,fa=fb=c
	│├─
	││●
	│├─
2 QED=	││Ra(fa)	1
	├─
1 CP	│a = b → Ra(fa)

4-4.

	│Rab ∨ Rcb	4
	│a = b ∧ gb = gc	2
	├─
	││Rbc
	│├─
2 Ext	││a = b	a=b,c,gb,gc
2 Ext	││gb = gc	a=b,c,gb=gc
	││
	│││¬ Rcb	(4)
	││├─
4 MTP	│││Rab
	│││○	a=b,gb=gc,Rbc,¬Rcb,Rab ⇏ ⊥
	││├─
	│││⊥	3
	│├─
3 CP	││Rcb	1
	├─
1 CP	│Rbc → Rcb