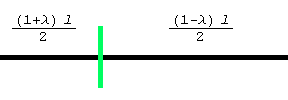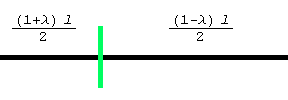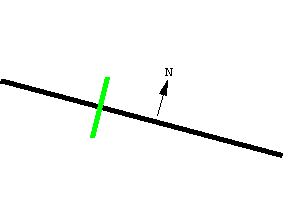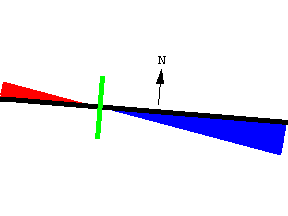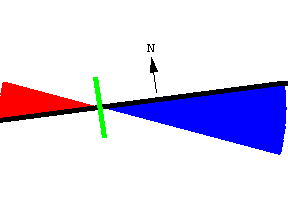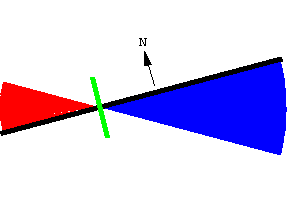
The area swept out consists of two circular sectors of different radii. The right and left radii are, respectively, (1-l) l /2  and   (1+l) l /2. Noting that one of the signed areas is positive and the other is negative, we get A = ¹/₂ ((1-l) l /2))² Dq  -  ¹/₂ ((1+l) l /2))² Dq. Multiplying this out and simplifying yields A = -¹/₂ l l² Dq.